F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de conoidibus et sphaeroidibus figuris Liber primus 9
<- App. -> <- = ->

PROPOSITIO IX.

Ellipsium areae sunt ad invicem, sicut rectangula, quae sub earum diametris compraehenduntur.

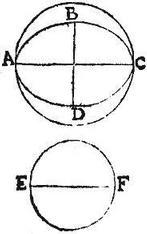
figura 9

Sunto duae quaelibet ellipses A, et B; sub ipsius A diametris contentum rectangulum sit CD; et sub ipsius B diametris sit EF. Dico iam quod area ellipsis A ad aream ellipsis B est sicut rectangulum CD ad rectangulum EF. Exponatur enim circulus quicumque G, ex cuius diametro quadratum sit HK: eritque per praecedentem, ellipsis A ad circulum G sicut rectangulum CD ad quadratum HK: itemque circulus G ad ellipsim B sicut quadratum HK ad rectangulum EF. Igitur ex aequali erit iam ellipsis A ad ellipsim B, sicut rectangulum CD ad rectangulum EF. Quod erat demonstrandum.

COROLLARIUM I.

Manifestum est ergo, quod similes ellipses sunt ad invicem sicut respondentium diametrorum quadrata.

COROLLARIUM II.

Ellipses autem, quarum diametri fuerint in proportione reciproca erunt ad invicem aequales. Quandoquidem huiusmodi ellipsium rectangula sub singularum diametris comprehensa aequalia sunt.

COROLLARIUM III.

Item ellipses, quarum una diameter unius uni diametro alterius fuerit aequalis sunt ad invicem sicut reliquae diametri: quoniam, et iisdem proportionalia sunt ellipsium rectangula, idemque de ellipsi, et circulo dicendum.

Inizio della pagina
 ->