[A:93r]

SPHAERICORUM EPITOME

1 Notandum quod Scientia Sphaeralium Triangulorum tota innititur doctrinae Sphaericorum Sphaerica elementa tradidit Theodosius libris tribus: in quorum primo agit de circulis maioribus, minoribus, et eorum polis. 2 Deque circulis per polos parallelorum, sive aequaliter inclinatus. In secundo de contactu et divisione circulorum, tam maiorum, quam minorum. De arcubus praeter polum ductis. 3 In tertio de collatione arcuum per parallelos sive circulos magnos divisorum. De triangulis Sphaeralibus acute scripsit Menaelaus, quem sequitur Ptolemeus libris tribus. In quorum Primo agit de arcubus et angulis et collatione Triangulorum Sphaeralium. 4 Angulis intrinsecis et exintrinsecis. In secundo de collatione arcuum abscisorum per circulos perpendiculares, sive aequaliter inclinatos. In tertio de sinuum arcuum proportione. De proprietatibus quibusdam trianguli sphaeralis orthogonii. 5 Nos quoque duo Sphaericorum libellos fecimus. In quorum primo de sinuum arcuum in triangulis proportione. In secundo Triangulorum sphaeralis orthogonii discussimus proprietates. Et in calce subiunximus practicam calculi. 6 Eius fundamenta demonstrantes, trium tabularum usus ad negocium applicato. Harum prima fuit Tabula sinus recti. Altera foecunda, quae Ioannes Regimontius invenit. Tertia Benefica, quam nos adiunximus. Per has absolvimus quaestiones, quae circa sphaeralia triangula proponi solent. 7 Et quoniam harum praecipue versuntur circa declinationes, ascensiones et caeteros primi mobilis arcus. Idcirco ad alleviandum calculi laborem, construximus tabulam generalem declinationum et ascensionum. Quae per calculum praedictum facile construitur. 8 Ut autem intelligatur modus et structura dictarum trium tabularum.

Esto triangulum abc habens angulum abc rectum. 9 In quo bd perpendiculares cadat ad latus ac cuius trianguli latera variantur ad libitum, servando angulum abc rectum. Positoque latere ab sinu toto, fiet bd sinus rectus anguli a. 10 Et da sinus eiusdem anguli secundus. Item posito ab gnomone fiet bc eius umbra versa: quae in tabula foecunda debetur angulo a. Adhuc latus ca erit radius, qui respondet eidem angulo a in tabula Benefica. [A:93v]

11 In triangulo abc angulus b rectus. Latus ab sinus totus in tabula sinus. Latus ab gnomon in tabula foecunda et in tabula Benefica. Latus bc umbra versa in tabula foecunda. 12 Latus ca radius in tabula Benefica. Angulus a cum quo intratur in quamlibet tabulam. Perpendicularis bd sinus rectus anguli a in tabula sinus. da sinus secundus eiusdem anguli a. Porro tabula sinus recti calculatur per doctrinam figurarum aequilaterarum in circulo et per doctrinam chordarum. 13 A quadrato sinus totus ab subtrahe quadratum sinus primi scilicet ba et supererit quadratum sinus secundi scilicet ad. Partire quadratus gnomonis per sinum secundum hoc est per hunc quadratum ipsius ab per sinum secundum da et exibit radius tabulae beneficae scilicet ca. 14 Multiplica sinum primum scilicet bd in sinum totum ab et productum partire in sinum secundum scilicet da et exibit bc umbra versa tabulae foecundae. Vel multiplica sinum primum scilicet bd in radium tabulae beneficae scilicet in ca et productum partire in sinum totum ab et prodibit bc umbra versa praedicta. 15 Exempli gratia si ponatur ab partium 100, fiet bc partium 75, cd partium 45, da partium 80. Tota ca partium 125. Angulus a graduum 36. Minutia 52 et paulo maior. Unde angulus c graduum 53 minutia 8. Et paulo minor. Quod simul graduum 90. 16 Quae omnia sequuntur ex similitudine triangulorum et proportionem linearum in triangulo abc. Quando igitur angulus a sit graduum 30 Tunc db sinus in tabula sinuum est dimidium ipsius ab. 17 Quod si ponatur angulus a rectus scilicet graduum 90 invenitur in tabula sinus totus hoc est ab semidiameter circuli. Et tunc umbra bc in tabula foecunda est infinita. Et radius ca in tabula benefica infinitus. Quando angulus a est dimidium recti scilicet graduum 45, tunc bc umbra in tabula foecunda est aequalis gnomoni ab. [A:94r] 18 Quando angulus a est graduum 60, tunc radius ca in tabula Benefica est duplus ad gnomonem ab quoniam scilicet tunc angulus c est 30 graduum. Quae omnia cuilibet vel mediocriter in Geometria erudito pervia sunt hactenus ad notitiam trium tabularum.

De tabula generali declinationum et ascensionum

19 Sit ab zodiacus ac aequator g punctum locus astri ab longitudo astri bg latitudo astri gh declinatio astri gc Argumentum declinationis. Unde sicut gc transit per polum zodiaci: ita gh per polum aequatoris. 20 Itaque cum arcu¹ ab longitudinis stellae sive arcu eclipticae inter punctum sectionis vicinioris a et locum longitudinis stellae b fit ingressus in tabulam generalem. Et primus arcus ibi inventus est bc Secundus autem angulus c. 21 Tertius autem ca arcus scilicet aequatoris inter sectionem et circulum latitudinis stellae.

Pro declinatione

Regula Prima

Et quoniam sicut sinus totus ad sinum anguli c sic sinus arcus gc angulo declinationis ad sinum gh declinationis astri. Idcirco ex regula quattuor quantitatum, notescet sinus gh et ipsa declinatio gh quaesita.

Pro ascensione recta

Regula Secunda

22 In descriptione praemissa, arcus ch aequatoris interiacens circulis latitudinis et declinationis stellae, dicitur differentia transitus stellae per coeli medium. Et quoniam sicut quadratus gnomonis ad rectangulo umbris versis gh declinationis et complementi anguli c. Sic est sinus totus ad sinum dicti arcus ch idcirco ex regula quattuor quantitatum, notescet sinus ch et ipse ch.

Tertia

23 Vel quoniam iam sinus totus ad radium declinationis ex tabula Benefica sumptum sic sinus secundus cg argumenti declinationis ad sinum secundum ch differentiae transitus [A:94v] stellae per coeli medium. Ideo notescit, sicut prius ipse sinus et eius arcus cuius complementum est arcus ch per quem notescit ascensio recta stellae.

Pro declinatione et ascensione recta puncti propositi in ecliptica.

24 Sit Ecliptica abe Aequator acd. Colurus solstitialis fed. Circulus declinationis fbc per punctum b propositum in ecliptica descendens a polo aequatoris f. Eritque bc arcus declinatio puncti b, de declinatio maxima et ascensio ipsius recta ac

Quarta

25 Et quoniam sint sinus totus ad sinum de maximae declinationis sic sinus arcus ab ad sinum arcus bc declinationis puncti propositi idcirco ex regula quattuor quantitatum notus erit sinus arcus bc et ipse arcus.

Quinta

26 Item quoniam sicut sinus totus ad sinum arcus cd sic est sinus arcus fb ad sinum arcus be ideo ex dicta regula notus erit sinus arcus cd et ipse arcus, et eius complementum ac ascensio puncti propositi.

Sexta

27 Vel quoniam sicut quadratus gnomonis ad rectangulo ex umbris versis arcuum bc et fe sic sinus totus ad sinum arcus ac ascensionis propositae. Ideo ex dicta regula notescet sinus arcus ac et ipse arcus.

Septima

28 Vel quoniam sicut sinus totus ad radium arcus bc in tabula Benefica repertum, sic sinus secundus ab ad sinum secundum ac ideo adhuc ex dicta regula patebit sinus secundus ac et ipse ac arcus.

Pro differentia ascensionali

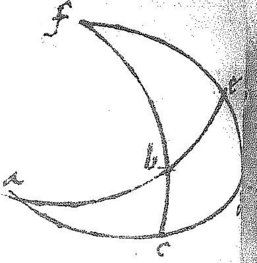
29 Sit acd aequator bc declinatio astri abe horizon obliquus ca differentia ascensionalis fbc horizon rectus ab latitudo fed meridianus ortus astri fe latitudo loci b locus astri. [A:95r]

Octava

30 Et quoniam, sicut quadratus gnomonis ad rectangulo ex umbris versis declinationis stellae bc et latitudinis loci fe sic sinus totus ad sinum arcus ca differentiae ascensionalis idcirco per regulam quattuor quantitatum, notus fiet sinus arcus ca et ipse arcus quaesitus.

Pro latitudine ortus astri

In eadem descriptione.

Nona

31 Quoniam sicut sinus totus ad radium arcus fe in tabula benefica sumptum: sic sinus bc declinationis ad sinum ab latitudinis ortus astri. Idcirco, per dictam regulam, notescet sinus arcus ab et ipse arcus quaesitus.

Pro differentia ascensionalis rursus

<Regula> Decima

32 Et quoniam, in eodem lineamento, sicut sinus totus ad radium arcus bc declinationis in tabula benefica, sic sinus be qui est sinus secundus latitudinis ortus be ad sinum cd qui est sinus secundus differentiae ascensionalis ac ideo ex dicta regula notus veniet sinus ipse secundus ac arcus et ipse arcus. 33 Quae omnia demonstrata sunt in libro Sphaericorum dudum memoratus. Hic repetita sunt ut pateat speculatio super quam innituntur regulae et animus lectoris quietior reddatur. Praeterea notandum quod numerus multiplicandus in tabula generali declinationum Ioannis Regimontii est sinus anguli sub circulo latitudinis stellae et aequatore compraehensus, qui fuit secundus arcus in nostra tabula generali decl. 34 Et ascen. Supposito sinu toto partium 100000. Radix ascensionum in tabula generali ascensionum Ioannis Regimontii est arcus aequatoris ab initio Arietis usque ad circulum latitudinis stellae secundum ordinem signorum sicut tertius arcus nostrae tabulae praedictae est arcus aequatoris a circulo latitudinis dicto ad viciniorem sectionem. 35 Denique numerus multiplicandus in tabula generali ascensionum Regimontii [A:95v] est productum ex 6 in umbram versam tabulae foecundae rendentem complemento anguli sub circulo latitudinis stellae et aequatore contenti. Quia sinus totus supponitur ab eo partium 60000. Haec aggregata sunt: ut in promptu sit speculatio et Praxis. 27 septembris 1571 36 Notandum quod tabellae tres scilicet sinus recti foecunda et benefica item et tabella generalis declinationum et ascensionum rectarum positae sunt superius cum Regulis in hoc quaternione cui nos hodie usuimus octo folia in principio cum indice contentorum et totidem hic in fine cum istac regularum repetitione et libellum mutatae membranae tegumento munivimus postridie. 37 Adducam exempla per singulas regulas. Stellae longitudo sit in 17 graduum latitudo septentrionalis graduum 5. Quaeritur eius declinatio Distantia puncti longitudinis a sectione proxima habet graduum 47, cum qua ingreditur tabula declinationum et ascensionum generalem, et excipio tres arcus. 38 Primum graduum 17 . Minutia 38. Secundum graduum 74, minutia 13. Tertium graduum 49, minutia 28. Iungo cum primo latitudinem loci quoniam ambo sunt septentrionalia et efficio graduum 22 minutia 38, cuius sinus partes 38483. Sinus autem arcus secundi partes 96230. Hos sinus multiplico unum in alterum et produco 3703219090 de quo abiicio quinque ad dextram figuras (sic enim dividitur in sinum totum) et sumpersit 37032, qui sinus est declinationis graduum 21 44 septentrionalis quaesitae. 39 Quoniam argumento² declinationis scilicet graduum 22 minutia 38 fuit septentrionale. Pro Secunda regula ut habeam ascensionem rectam dictae stellae, multiplico umbram versam declinationis scilicet 39898 in umbram versam complementi anguli hoc est arcus secundi quod complementum est graduum 15 minutia 47 quae umbra est 28267 et produco 1127796766, de quo abiectis quinque figuras ultimas supersit 11278, cui sinui rendent graduum 6 minutia 28 differentia transitus stellae per coeli medium. 40 Quam subtraho de arcu tertio graduum 49 28 et relinquuntur graduum 43 0 ascensio scilicet recta stellae praedictae. [A:96r] Pro Tertia regula sumo cum gradibus 21 minutiis 44 declinationis ex tabula benefica radium partes 107657 quem multiplico in sinum secundum argumenti declinationis graduum 22 38 hoc est in sinum eius complementi graduum 6722, qui sinus est fere partes 92300 et produco 9936741100, de quo ablatis 5 figuras supersunt 99367 cui sinui rendet arcus graduum 83 minutia 33 cuius complementum graduum 6 minutia 27 differentia transitus stellae per coeli medium³ per quam elicio ascensionem rectam graduum 43 0 sicut in praecedenti regula. 41 Pro Quarta regula ut habeam declinationem pro 10 gradum distantiae a sectione proxima graduum 40 sinum scilicet partes 64279. Multiplico in sinum maximae declinationis graduum 23 1/2 scilicet partes 39875 et produco 2563125125. Unde abiicio 5 figuras sic enim fit divisio in sinum totum et restant partes 25631 cui sinui rendent declinatio quaesita graduum 14 minutia 51. 42 Pro Quinta regula, ut habeam ascensionem rectam dicti puncti sinum secundum graduum 40 scilicet 76604. Multiplico in sinum totum et produco 7660440000 quod partior in sinum secundum declinationis graduum 14 minutia 51 scilicet 96660 et exeunt partes 74252, cuius sinus arcus est graduum 5224, qui ablatus a quadrante residuat graduum 37 minutia 36 ascensionem rectam dicti puncti. 43 Pro Sexta regula ut habeam eandem ascensionem rectam, sine fastidio talis divisionis. Cum complemento maximae declinationis graduum 66 1/2 sumo numerum ex tabula foecunda 230094 et cum declinatione graduum 14 minutia 51. 44 Sumo numerum ex eadem tabula 26514 quos multiplico invicem, et produco 61009 sinus scilicet ascensionis rectae, quam quaerimus graduum 37 minutia 36 ut prius. Pro Septima regula ad eandem ascensionem rectam aliter per tabulam beneficam declinationis graduum 1451 radium ex tabula dicta scilicet 103458 sumptum multiplico in partes 76604 sinum secundum graduum 40. 45 Hoc est sinum graduum 50. Et produco 7925296632. Unde proiectis 5 figuris postremis excipio reliquas partes 79253 cuius sinus arcum invenio graduum 52 minutia 25 cuius complementum est graduum 37 minutia 35 ascensio recta, ut prius. Nec mireris alicuius minutiae differentiam: quam inducit ingressus et partis proportionalis, quae non ad amussim ut ratio posat, deciditur⁴ calculus. [A:96v] 46 Pro Octava regula ad habendam differentiam ascensionalem ad latitudinem graduum 38 1/6 cum declinatione graduum 23 1/2 umbram versam graduum 38 1/6 ex tabula foecunda scilicet partes 78604. Multiplico in umbram versam graduum 23 1/2 scilicet partes 43485 et produco 3418094940. Unde segrego quinque postremas figuras et relinquuntur 34181 sinus scilicet differentiae ascensionalis graduum 19 minutia 59 qua quaeritur. 47 Pro Nona regula ad habendam latitudinem ortus pro iisdem latitudine et declinatione radium graduum 38 1/6 latitudinis ex tabula benefica, scilicet 127198. Multiplico in sinum declinationis graduum 23 1/2 scilicet 39875 et produco 5072020250. Ex quibus separo quinque figuras: et relinquuntur partes 50720 sinus latitudinis ortus quaesitae scilicet graduum 30 minutia 29 arcus scilicet horizontis inter aequatorem et solem apud tropicum exorientem. 48 Pro Decima Tandem regula ad habendam aliter differentiam ascensionalem Radium declinationis graduum 23 1/2 scilicet partes 109050 ex tabula benefica sumptum multiplico in sinum secundum latitudinis ortus graduum 30 minutia 29 hoc est⁵ in sinum graduum 59 minutia 31 qui partes habet 86178. Et produco 9397710900. Unde se pono quinque ultimas figuras et restant partes 93977 cui sinui respondet arcus graduum 70 minutia 1 cuius complementum graduum 19 minutia 59 differentia ascensionalis quaesita, quae prius. 49 Quae ad tempus aequinoctiale reducta, conflat paulominus quam horam et 1/3 excessum semidiurni maximi in horizonte latitudinis graduum 38 1/6 supra semidiurnum aequinoctialem. Ad summam hae quaestiones et aliae compraetes absolvi poterant per tabulam sinuum sed tabula foecunda et tabula benefica adiectae sunt, ad facilitatem calculi: et ad evitandum laborem divisionis. Nam calculantibus multo facilior est multiplicatio, quam divisio. Primo octobris 1571 50 Sub his exemplis diriges calculum tuum ad similes quaestiones, pro quovis stella, pro quolibet coeli puncto. Sequitur exemplorum brevis repetitio. [A:97r] graduum 17 distat a sectione graduum 47 cum quo ex tabula generali eligitur tres arcus: primus graduum 17 minutia 38 secundus graduum 74 minutia 13 tertius graduum 49 minutia 28. Cuius sinus partes 38483 sinus arcus secundi partes 96230. Horum productum 3703219090. Unde abiectis 5 figuris residuatur 37032 cuius sinus arcus graduum 21 minutia 44 declinatio sep. 51 Pro dicto puncto umbra versa declinationis partes 39898. Umbra versa graduum 15 minutia 47 complementi arcus secundi partes 28267 Harum productum 1127796766. Unde partes 11278. Sinus posat arcum graduum 6 minutia 28. Differentia transitus per coeli medium qui ablatus de tertio arcu g. 49 m. 28. Residuat graduum 43 minutia 0 ascensionem rectam. Idem aliter pro graduum 21 minutia 44. Radius tabula beneficae partes 107657 pro graduum 67 Minutia 22 complemento argumentis declinationis partes fere 92300. 52 Horum productum 9936741100. Unde partes 99367 habent pro sinu graduum 83 minutia 33 huius arcus complementum graduum 6 minutia 27 praedicta differentia. Pro declinatione 10 graduum distantia a sectione graduum 40 eius sinus partes 64279 sinus maximae declinationis graduum 23 1/2 partes 39875. Horum productum 2563125125. Ergo partes 25631 est sinus declinationis quaesitae graduum 14 minutia 51. 53 Pro ascensione recta dicti puncti sinus secundus graduum 40 habet partes 76604 qui ductus in sinum secundum decl. Scilicet graduum 75 minutia 9 exhibet partes 79252 cuius arcus graduum 52 minutia 24 ablatus a quadrante residuat graduum 37 minutia 36 ascensionem quaesitam. Idem aliter complementi maximae declinationis scilicet graduum 66 1/2 umbra versa partes 230094. 54 Umbra versa declinationis graduum 14 minutia 51 partes 26514. Quarum productum 6100942410. Unde partes 61009. Sinus graduum 37 minutia 36 ascensionis rectae. 55 Idem adhuc aliter declinationis graduum 14 minutia 51 radius ex tabula benefica partes 103458. Sinus secundus graduum 40 partes 76604. Horum productum 7925296632 unde partes 79253 habent arcum graduum 52 minutia 25 cuius complementum graduum 37 minutia 35 ascensione recta. 56 Pro differentia ascensionalis latitudine graduum 38 1/6 cuius umbra versa partes 78604, declinationis graduum 23 1/2 umbra versa partes 43485. productum 3418094940. Unde partes 34181 sinus habet graduum 19 minutia 59, differentiam ascensionalem. Pro latitudine ortus radius ex tabula benefica pro gradibus 38 1/6 habet partes 127198. Sinus declinationis graduum 23 1/2 est partes 39875. Horum productum 5072020250. Unde partes 50720 sinus latitudinis ortus scilicet graduum 30 minutia 29. 57 Aliter pro differentia ascensionalis graduum 23 1/2 radius ex tabula benefica partes 109050. sinus secundus latitudinis ortus scilicet sinus graduum 59 minutia 31 habet partes 86178. Quorum productum 9397710900. Unde partes 93977 sinus sunt graduum 70 minutia 1 cuius complementum graduum 19 minutia 59 differentia ascensionalis ut prius. Postridie