THEOREMA XXXI

102 Si in cavum speculum a signo quopiam[C:21v] tres radii incidant, unus quidem per centrum, duo vero a centro inaequaliter remoti, horum qui remotior est, inferius cum eo, qui per centrum, concurret.

103 In cavum speculum³⁶⁵ AB a signo C cadant radii CD, in quo centrum speculi E, at³⁶⁶ CF, CG inaequaliter a centro remoti; sitque³⁶⁷ remotior CG, et CF reflectatur ad CD in signo H. Aio quod CG³⁶⁸ reflexus infra signum H ipsi CD³⁶⁹ concurret. Connectatur³⁷⁰ enim GH, et a centro E cadant³⁷¹ ad ipsas CF et CG perpendiculares³⁷² EK et EL. Deinde ipsis FH et GH³⁷³ productis occurrant perpendiculares EM³⁷⁴ et EN, atque ab ipsis³⁷⁵ F et G signis exeant tandem ipsi CD perpendiculares FP et GO. Eritque maior ipsius CF ad CE ratio quam³⁷⁶ ipsius GC ad CE, per 8 V³⁷⁷. Sed propter triangulorum³⁷⁸ similitudinem FCP³⁷⁹, ECK, ut CF ad FP, sic CE ad EK, per 4 VI. Ergo alternando per 16 V sicut CF³⁸⁰ ad CE, sic FP ad EK³⁸¹ et ideo ad EM, quandoquidem EK et EM³⁸², propter aequos inflexionum angulos AFK et MFB, aequas sibi invicem esse necesse est.³⁸³ Et³⁸⁴ sicut GC ad CE, sic GO ad EL. Ergo maior est [S:26]FP ad EM quam GO ad EL.[C:22r] Et ideo³⁸⁵ propter triangulorum ³⁸⁶ similitudinem maior FH ad HE quam GO ad EL. Sed GH maior est quam FH. Ergo a fortiori GH ad HE maior quam GO ad EL. Et ideo³⁸⁷ propter similitudinem triangulorum, GO ad EN maior quam GO ad EL. Quare maior est EL quam EN. Unde necesse fiet³⁸⁸, ut maior sit angulus HGB quam angulus CGA³⁸⁹.³⁹⁰ Quamobrem CG reflectetur ad CD infra signum H.

104 Quod si contingerit³⁹¹ EH ipsi HG perpendicularem esse, ut in secunda descriptione, similiter ostendemus quod maior GH ad HE quam GH ad EL. Et ideo³⁹² maiorem esse EL quam EH. Quare eadem, qua supra, ratione CG radius³⁹³ ad CD concurret infra signum H.

105 Quod si contigerit EH ipsi FH perpendicularem esse, ut in tertia figura, tunc, quoniam EK et EH propter aequos inflexionum angulos aequales sunt; et EL maior quam EK; ipsa vero EH maior quam EN, ideo maior est EL quam EN. Et ideo³⁹⁴ sicut antea CG ad CD infra signum H reflectetur.

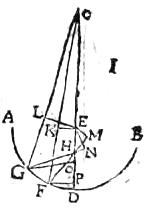
106 Si vero perpendiculares EM et EN, ut in quarta figura a partibus F, G ceciderint, tunc, quoniam EK et EN per hypoth. aequales; et EK minor quam EL; sed EM maior quam EN³⁹⁵, ideo maior[C:22v] erit EL quam EN. Quare ut prius CG ad CD infra signum H reflectetur.

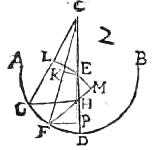
107 Postremo, si ut in quinto typo, perpendicularium EM et EN, ipsa EM ad partes B, ipsa vero EN ad partes A ceciderit, tunc ductis perpendicularibus, ut in prima descriptione non aliter quam ibi, ostendemus maiorem habere rationem GO ad EN quam GO ad EL, et ideo³⁹⁶ maiorem esse EL quam EN. Quare et CG ad³⁹⁷ CD infra signum H reflectetur. Quod erat ostendendum.

Corollarium

108 Si ergo a signo quopiam ad cavum speculum per centrum [S:27] ad duorum³⁹⁸ circulorum inaequalium parallelorum polum radius ceciderit³⁹⁹, quicumque radii ab eodem signo ad circulorum periferias ceciderint, a circulo minore⁴⁰⁰ ad verticem unum in eo qui⁴⁰¹ per centrum radio, a maiore vero ad signum inferius in eodem radio concurrent; eruntque ab⁴⁰² his duobus circulis⁴⁰³ reflexi radii duae conicae superficies, quarum altera secabit alteram, et etiam sectio circulus utrique superficiei communis. Patet hoc corollarium partim ex praemissae corollario⁴⁰⁴, partim ex praesenti theoremate sequenti.[C:23r]