[S:16]

THEOREMA XXII

65 Lucidorum per foramen in planum quodpiam radiantium formae conversae porriguntur. Hoc enim, ut in praemissa, fit ex radiorum intersectione. Quod ut distinctius pateat, quasdam descriptiones adducemus.

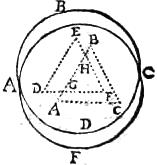
66 Pro lucido enim circulari intelligantur¹⁶⁹ supra bases AB atque CD duo coni similes, verticem sortiti eundem qui sit¹⁷⁰ E signum, sintque eorum axes una recta, quo fiet ut quaecumque recta ab ipsius AB basis circumferentia¹⁷¹ ad E verticem agatur, eadem ulterius producta ad ipsius DC¹⁷² basis periferiam perveniat, ideoque una erit ipsa AC recta. Itemque una ipsa BD. Secetur itaque DEC conus plano ipsi AB, ideoque¹⁷³ ipsi DC circulo parallelo, sitque sectio circulus GF. Intelligatur ergo, per foramen GF circulare, lucidum AB circulare in planum[C:13v] DC radiare. Eritque circulus DC tantum ex ipso plano a lucido AB illuminatus. Ab ipso enim lucido AB in nullum ipsius DC plani signum extra ipsum DC circulum radius elabitur. Et quoniam A in C, et B in D radiat, ideo¹⁷⁴ ipsius AB circuli figura conversa est. Concludimus ergo quod¹⁷⁵ circulare lucidum per circulare foramen¹⁷⁶ sibi aeque distans conum protendit luminosum, cuius vertex inter lucidum ipsum et foramen existit.

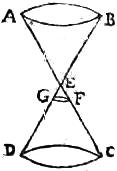
67 Pro lucido etiam alterius formae, ut triangulo, intelligantur supra ABC et DEF triangula similia duae similes pyramides verticem eundem habentes, qui sit G, signum, sitque unaquaeque ipsarum AD, BE et CF linearum¹⁷⁷ sese in signo G secantium una recta. Quo fiet ut ipsum AB latus ipsi DE, ipsum autem BC ipsi EF, ipsum vero CA ipsi FD respondeat. Utque ipsa AGB et DGE, item et ipsa BGC et EGF triangula, nec non et ipsa CGA¹⁷⁸ et FGD triangula bina, in uno sunt¹⁷⁹ plano. Omnis igitur a quolibet¹⁸⁰ ipsius ABC trianguli¹⁸¹ latere et per G signum acta¹⁸² linea ad trianguli DEF illi respondens perveniet¹⁸³ latus. Secetur itaque DEFG pyramis plano parallelo basi¹⁸⁴ DEF, sitque sectio triangulum HKL ipsi DEF, ideoque¹⁸⁵ ipsi ABC simile. Et intelligatur triangulum ABC lucidum per triangulare¹⁸⁶ foramen HKL in planum[C:14r] DEF ra[S:17]diare . Eritque ex plano DEF triangulum dumtaxat DEF ab ipso ABC lucido illuminatum. Nullus enim ab ipso lucido ABC in planum DEF extra ipsum triangulum DEF radius progreditur. Et quoniam latus AB in latus quidem DE, latus vero BC in ipsum EF, ipsum vero CA in ipsum FD, radiat, ideo ipsius ABC trianguli¹⁸⁷ forma, quae¹⁸⁸ ipsum DEF triangulum est, ipsi lucido ABC conversa videtur. Concludimus ergo quod rectilineum lucidum per foramen sibi simile et parallelum¹⁸⁹ ac conversim positum radians, luminosam extendit pyramidem, cuius vertex ipsi lucido et foramini interiacet.

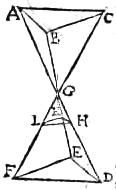
68 Sit quoque lucidum qualecumque AB, et foramen qualiscumque formae CD. Et productis in ipsum FE planum ipsis ADE, et BCF radiis sese in G signo secantibus, item ipsis ACH et BDK, intelligantur FCH et KDE luminosae pyramides vertices habentes C et D, bases vero FH et KE. Quo fiet ut si ipsi AB parallelum¹⁹⁰ ponatur FE planum, utraque ipsarum FH et KE basium ipsi AB lucido similis existat propter pyramidum similitudinem. Quoniam igitur ipsi FCH et KDE anguli maiores sunt angulis FBK et HAE, ideo fit ut productis radiis, ipsa FH et KE basium spatia non proportionaliter crescant cum ipsis FK et HE spatiis¹⁹¹. Nam quo ulterius radii producti fuerint, eo maior fiet ipsorum FH et KE spatiorum proportio ad ipsa FK et HE¹⁹² spatia.¹⁹³ [C:14v] Poterunt ergo eo usque produci radii, ut ipsa FK et HE spatia respectu ipsorum FH et KE spatiorum¹⁹⁴ insensibilia fiant. Sed¹⁹⁵ ipsa FK et HE¹⁹⁶ spatia¹⁹⁷ distantiae sunt pyramidarum ipsarum FH et KE basium, quae¹⁹⁸ ipsius AB lucidi formae sunt. Ergo per praemissam, quo magis producti fuerint radii, eo magis ipsae FH et KE bases ad unius ipsarum, ideoque¹⁹⁹ ad ipsius AB lucidi similitudinem accedent, quandoquidem ipsae²⁰⁰ FH²⁰¹ et KE figurae similiter positae sunt. Et per praedictae corollarium poterunt eo usque produci radii, ut ipsarum FH et KE figurarum una esse putetur²⁰².

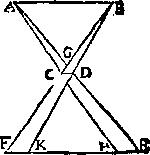
69 Quod eo magis fiet, quo²⁰³ ipsum CD foramen respectu ipsius AB lucidi minus fuerit. Item quo magis AB lucidum a foramine CD remotum fuerit, tanto ipsa FK et HE²⁰⁴ repectu ipsorum FH et KE spatiorum minora fient. Similiter ostendemus quod [S:18] forma FE a pyramide FGE, quae maxima est, et aliae infinitae ab infinitis pyramidibus profectae²⁰⁵ paulatim in progressu coeunt, et ad ipsius AB lucidi similitudinem accedunt, donec ipsi fere lucido similem²⁰⁶ conficiant figuram. Concludimus ergo quod quo magis a quocumque lucido per qualecumque²⁰⁷ foramen radiante processerint radii, eo magis in planum, quod lucido parallelum est, profectum²⁰⁸ lumen ad ipsius lucidi similitudinem[C:15r] accedit. Et tandem sensu decepto, ipsi simile videtur, et in situ conversum, velut²⁰⁹ ex radiorum intersectione patet. Verum ergo fuit quod speculatio nostra conclusit.

Corollaria²¹⁰

70 1²¹¹ Hinc illud sequitur, ut sole per qualecumque foramen radiante, quo longius a foramine radii processerint, eo magis in planum circulo, qui terminus est radiantis superficiei, parallelum, proiecta lux ad eiusdem²¹² circuli formam propius accedat, ac²¹³ tandem sensu decepto, perfecte²¹⁴ circularis appareat. quandoquidem²¹⁵ omne²¹⁶ foramen, quod solari radio transitum praebere solet, tam respectu solaris magnitudinis quam distantiae, insensibilis sit quantitatis.

71 2²¹⁷ Similiter necesse est, ut luna per²¹⁸ qualecumque foramen radiante, quo magis a foramine radii abscesserint, eo magis in planum radianti plano parallelum proiecta lux ad lunaris formae similitudinem accedat, ac tandem ipsi fere similis²¹⁹ fiat²²⁰. Hoc idem dicendum est de sole partim caligante. Nam tunc lux per foramen transmissa proiicit in planum oppositum²²¹ formam dimidiati solis. Idem ipsum dicendum est de sole, vel partim exorto vel partim sub horizontem²²² immerso.²²³

72 [C:15v] 3²²⁴ Quod si planum non fuerit radianti formae parallelum, proiectam lucem ipsi lucido similem²²⁵ non fieri monstratum est. Velut²²⁶ cum solis lux per foramen ingrediens, quae paulatim conica sit²²⁷, in obliquum porrecta planum, formam efficit quae conica sectio est.

73 4²²⁸ Illud quoque nequaquam praetereundum quod lucido et plano a foramine aequaliter distantibus proiecta in planum lux ipsi lucido aequalis apparet; lucido vero magis distante, minor; minus vero²²⁹, maior, foramine tamen insensibilem respectu lucidi magnitudinem habente. Unde si solares radii [S:19] seu lux tantum²³⁰ a foramine procederent, quantum sol ipse a foramine removetur, proiicerent²³¹ circulum circulo²³², qui terminat radiantem superficiem, aequalem; ac si magis, maiorem. Sed quoniam nunc semper minus, ideo²³³ minorem.

74 5²³⁴ Lucidum igitur per foramen aliquod radians infinitas proiicit pyramides, quae, quoniam²³⁵ crescunt intervallis inter superficies non ad eandem proportionem crescentibus, ideo²³⁶ paulatim in unam coeunt, donec omnes una fiunt pyramis, superficierum intervallo unitaeque²³⁷ pyramidis formam insensibiliter variante²³⁸ per praedicta corollaria.[C:16r]

75 6²³⁹ Illa quoque iucunda speculatio non est oblivioni mandanda, quod lucidum per duo vel plura foramina radians, innumeras per eadem proiicit pyramides, quae quoniam crescunt, ingrediuntur²⁴⁰ alia in aliam, et commistae tandem in unam coeunt, uniusque formam acquirunt, intervallo tamen ad pyramidum²⁴¹ magnitudinem insensibili existente. Unde necesse est solis lumen per duo vel quotlibet foramina²⁴² ingrediens, totidem per eadem proiicere²⁴³ circulares formas, quae paulatim commixtae coeunt, unumque tandem visui ostendunt circulum. Quod quidem non aliter ostendetur quam de luce per unum transeunte foramen nuper ostensum est.