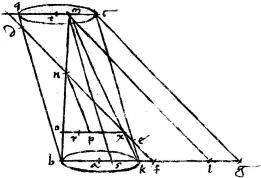
7a Cylindro proposito, sectoque ellipsi, super eandem basim idemque fastigium conum constituere, qui sectus eodem, quo cylindrus, plano ellipsim faciat similem ellipsi cylindricae.
Cylindrus esto, cuius axis at et bases circuli bk qc primarium parallelogrammum bqck in quo prima diameter ellipsis sit de.
Oportet super basim bak conum erigere sub cylindri bc celsitudine, qui sectus plano ellipsis de faciat ellipsim similem ellipsi de.
Producatur31 recta de utrinque donec occurrat ipsis bk qc apud signa f h item compleatur parallelogrammum fhcg.
Quibus peractis, per 28am 6i super rectam bk constituatur rectangulum equum quadrato kg excedens specie a quadrato. Sitque latitudo excessus kl erit quippe, per praecedentem, kl maior quam kf minor vero quam kg cum bk non sit maior, quam hc et ideo quam fg.
Agatur itaque ipsis fh gc parallelus, lm ipsi hc occurrens ad signum m sub quo vertice superque basim bk erigatur conus bmk qui sectus quodam parallelogrammo bc faciat triangulum bmk sectus vero plano ellipsis de faciat ellipsim, cuius prima diameter erit n![]() 32 quae scilicet est ex diametro de inter puncta n
32 quae scilicet est ex diametro de inter puncta n ![]() in quibus bm mk secantur ab ipsa de.
in quibus bm mk secantur ab ipsa de.
Aio itaque quod ellipsis conica n![]() similis est ellipsi cylindricae de quod sic ostendatur.
similis est ellipsi cylindricae de quod sic ostendatur.
Quoniam rectangulum kl lb aequum est per hypothesim quadrato gk ideo per 16am sexti lk kg lb sunt continue proportionales: sit itaque ipsi bg parallelus ![]() o et np parallelus ipsi mk et occurrens ipsi
o et np parallelus ipsi mk et occurrens ipsi ![]() o apud p.
o apud p.
Item inter ![]() p
p ![]() o media proportionalis sit
o media proportionalis sit ![]() r eritque per 71am primi Conicorum elementorum
r eritque per 71am primi Conicorum elementorum ![]() r secunda diametros ellipsis n
r secunda diametros ellipsis n![]() . Adhuc a puncto m veniat ipsis ck qb parallelus ms et reliqua, quae sequuntur in antepraemissa, eritque eodem penitus processu, sicut de prima diametros ellipsis de ad bk secundam eiusdem diametrum, sic n
. Adhuc a puncto m veniat ipsis ck qb parallelus ms et reliqua, quae sequuntur in antepraemissa, eritque eodem penitus processu, sicut de prima diametros ellipsis de ad bk secundam eiusdem diametrum, sic n![]() prima diameter ellipsis n
prima diameter ellipsis n![]() ad
ad ![]() r secundam eiusdem diametrum: quare, per primam huius ellipsis conica n
r secundam eiusdem diametrum: quare, per primam huius ellipsis conica n![]() et ellipsis cylindrica de sunt similes. Itaque super basim bk cylindri bc sub ipsius cylindri celsitudinem erectus est conus bmk qui sectus plano secundario quo cylindrus bc facit ellipsim n
et ellipsis cylindrica de sunt similes. Itaque super basim bk cylindri bc sub ipsius cylindri celsitudinem erectus est conus bmk qui sectus plano secundario quo cylindrus bc facit ellipsim n![]() similem cylindricae ellipsi de quod faciendum proponebatur.
similem cylindricae ellipsi de quod faciendum proponebatur.
Scholium <a>
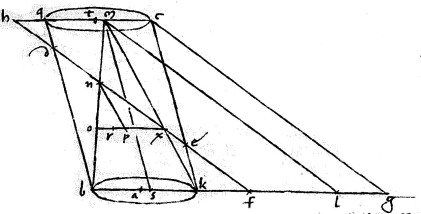
Illud autem est animadversione dignum quod quonamsi lk kg lb in proportione33 sunt34 continua, ideo per 14am 2i Conicorum bk differentia primae et tertiae dictarum linearum maior est quam dupla ipsius lg differentiae primae et secundae et ideo maior quam dupla ipsius cm vel sk quare vertex conicus m numquam coincidet centro t circuli qc semperque cadet inter puncta t c.
Scholium <b>
Attendendum quod, cum per corollarium 4ae huius, omni ellipsi cylindricae inveniatur similis nec non similis et aequalis ellipsis conica: quidquid in Conicis elementis demonstratum est de conica35 ellipsi, idem item cylindrica ellipsi concludi potest non ergo fuit necessarium hic universas ellipsis proprietates ostendere cum in conicis ostensae sint.
Praeterea hi duo cylindricorum libelli, instaurati sunt labore et industria Francisci Maurolycii mathematicae disciplinae studiosissimi: si quid autem repertum fuerit in quopiam exemplari, quod hic desidereretur, aut quidpiam magis authoris menti, consentaneum, hic36 protinus resarciatur.
LIBELLI SECUNDI CYLINDRICORUM SERENI FINIS *
Messanae in freto siculo manu et industria Francisci Maurolycii .16o. augusti 1534 * * * * * *