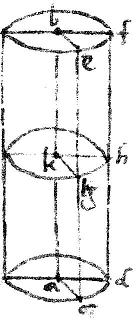
13^am30 Si cylindrus plano secetur parallelo basibus: sectio circulus est centrum habens in axe.

Cylindrus cuius bases circuli circum centra a b qui sint cd ef axisque ab secetur plano gkh ipsis cd ef circulis parallelo: sitque facta in cylindro sectio gh³¹.

Aio quod sectio gh³² circulus est; eiusque centrum k punctum per quod transit axis ab.

Capiantur enim in periferia gh³³ duo quaevis puncta utpote g h per quae ducantur, per praecedentem³⁴, latera cylindrica dhf egc³⁵ et connectantur bf kh ad be kg ac³⁶ eruntque per corollarium praemissae³⁷, ipsae ab df paralleli; et per 16^am 11ⁱ ipsae bf kh ad³⁸ paralleli; nec secus ipsae ab ce paralleli, et ipsae be kg ac paralleli: parallelogramma ergo sunt bg bh itaque³⁹ per 34^amprimi ipsae be kg aequales, nec non ipsae bf kh aequales: sed per diffinitionem circuli, ipsae be bf⁴⁰ aequales: igitur ipsae hk kg aequales: non aliter ostendam quod omnes rectae a puncto k ad periferiam sectionis gh sunt invicem aequales: ergo per conversionem diffinitionis circuli gh⁴¹ sectio circulus est, cuius centrum k punctum quod est propositum. Hic sequitur⁴² propositio infra posita.

Additio post. 13^am43

Duo plana aequidistantia non ei quod per axem parallela cylindrum secantia similes et aequales faciunt sectiones.

Nam ductis planis per axem et eis, quae per axem, parallelis, diametri sectionium et diametris paralleli erunt latera opposta parallelogrammorum et ideo aequalia, quare sectio sectioni congruet undique et ideo erunt similes et aequales; quod est propositum.