[A:1r] [a:19r] DEMONSTRATIO ALGEBRAE¹

1 Multae quaestiones in calculo solvi possunt per positionem ut, supposita quantitate quaesiti per nomen adhuc ignotum, ad eius postea notitiam perveniatur. Regulae autem quaedam sunt² positionum: quas Arabes inventores Algebra dicunt. Cuius terminos intelligere operae precium est. Utuntur³ hac regula nonnulli magnae authoritatis viri de quorum numero est Jo. de monte regio, in opere, quod scripsit contra Cusae quadraturam. 2 Sicut itaque⁴ unitas, radix, quadratum, cubus, quadratum secundum⁵ sunt in proportione continua⁶: ita et algebrae authores⁷ ponunt terminos suos continue proportionales qui sunt⁸ numerus, res, census, cubus, census secundus et sequentes in infinitum dignitates, vocabulis deficientibus; quod et in⁹ numeris accidit. Nam cum processus fiat in infinitum¹⁰, nomina omnino deficiunt.

3 Itaque numerus est omnis quantitas cognita; quae toties positam continet, unitates habet numerus eam representans¹¹. Res autem est quantitas terminata, sic vocata, dum ignota est. Haec in se ducta producit censum. Res autem censum multiplicans producit cubum. Et cubum multiplicans generat censum secundum. 4 Quippe qui ex censu in se ducto consurgit. Ut enim in Elementis ostensum est, in ordinem harum dignitatum (quae sunt in proportione continua) unaquaeque ipsarum in se ducta producit id, quod fit ex ductu duarum collateralium, vel¹² ex ductu duarum ab illa aequaliter hinc et inde¹³ distantium. 5 Et ideo utraque producit totam a se, quota est ipsa ab unitate. Quia unitas in illam producit eandem. Item et [A:1v] duae quaelibet se invicem multiplicantes producunt illud, quod fit ex ductu duarum collateralium, vel ex ductu duarum ab illis aequaliter utrinque¹⁴ distantium. 6 Unde semper ex ductu alicuius earum in se, vel ex ductu duarum quarumlibet, producitur aliqua, quae in ordine ipsarum invenitur. Et quoniam unitas, quae numeri nomen sortitur, est in ordine ipsarum, idcirco proportio continuata ipsarum erit aliqua ex multiplicibus ut dupla, tripla, quadrupla, quincupla et deinceps; tam scilicet crescendo supra unitatem, quam infra eam in simili proportione frangendo. Exempli gratia in proportione quincupla:

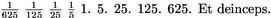
Potest¹⁵ esse et alia, quam multiplex proportio: ubi fractio aliter poscit.

[a:19v] 7 Quandocunque igitur in calculo cognoscitur aliqua aequalitas inter has dignitates licebit inde coniicere quantitatem, seu valorem, seu precium rei, quae ponebatur pro quantitate quaesita, atque ita satisfieri propositae quaestioni. Sed talis aequalitas attenditur sive in collatione duarum dignitatum collateralium¹⁶, sive per aliquam vel aliquot medias aequaliter¹⁷ distantium. 8 Et pro tali aequalitate datur prima regula. Aut aequalitas intelligitur cum aggregatum duarum dignitatum fuerit aequale alteri ex dignitatibus¹⁸, ita tamen ut tales tres dignitates sint aut collaterales aut aequaliter (hoc est per singulas vel totidem medias) remotae. 9 Itaque si minimae et mediae [A:2r] congeries conferatur maximae, dabitur in eo casu secunda regula. Si vero¹⁹ minimae et maximae aggregatio aequiperet mediam²⁰, fiet tunc tertia regula. Si demum²¹ mediae et maximae cumulus adaequetur minimae²², tunc assignabitur quarta regula.

10 Exemplum primae regulae: ut si numerus sit aequalis rebus²³, vel si res adaequent²⁴ censum, vel si²⁵ res aequiperent²⁶ cubum, vel una quaelibet unam quamlibet dignitatem. Exemplum secundae regulae. Ut si numerus cum rebus adaequaverint censum; vel si res cum censu valeant cubum. Et ita de reliquis dignitatibus collateralibus. 11 Vel si numerus cum censu aequivaleant censum secundum. Et ita de reliquis dignitatibus per unam vel totidem medias aequidistantibus. Exemplum tertiae regulae. Ut si numerus cum censu adaequaverint²⁷ rem. Vel si res cum cubo aequiperent censum. Et sic pro tribus quibuscumque dignitatibus collateralibus. 12 Vel si numerus cum censu secundo aequivaleant censum. Et ita de reliquis per unam vel totidem medias disterminatis. Exemplum quartae regulae, ut si res cum censu adaequent numerum. Vel si census cum cubo valeat rem. Et similiter pro tribus aliis collateralibus. Vel si census cum censu secundo aequiperent numerum. Nec secus pro tribus quibusvis per unam vel totidem medias distinctis.

[A:2v] [a:20r] 13 Docebo nunc, quo pacto ex aequalitate dignitatum inter calculandum occurrente, notescat quantitas, valor seu precium rei quaesitae²⁸: atque ita satisfiat quaestioni regulas²⁹ demonstrans et pro singulis exemplum adducens congruum.

Prima Regula

14 Cum duae dignitates fuerint inter se aequales, partire minorem per maiorem. Nam quod exibit ex divisione, erit precium rei, si dignitates sunt collaterales. Si autem distent per unam mediam: tunc eius, quod exibit ex divisione³⁰, radix quadrata fiet precium rei. Si vero distent per duas medias: tunc eius, quod exibit, radix cubica erit precium rei.

15 Exempli gratia, sint 2 res aequales numero 10: partior 10 per 2, et proveniunt 5 precium scilicet rei. Item si 2 census sunt aequales 10 rebus idem precium proveniet. Sic etiam si duo cubi fuerint aequales 10 censibus. Namque sicut res ad unitatem, ita tam census ad rem, quam cubus ad censum, in hoc casu quincuplus est. 16 Quod si 2 census sint aequales numero 50, vel si 2 cubi res 50 adaequaverint: partior tunc 50 per 2 et proveniunt 25. Cuius radix quadrata scilicet 5, tunc fit precium rei, quoniam collatae dignitates per unam mediam distant. Quod ideo fit quoniam proportio dignitatum³¹ distantium per unam mediam dupla est ad proportionem collateralium. 17 Et sicut ex divisione illarum provenit res, ita ex partitione harum provenit quadratum rei, hoc est census. At si 2 cubi aequiperent numerum 250, nunc (quoniam duae mediae interiacent dignitatibus) ex divisione 250 [A:3r] per 2³² provenient 125 cubus scilicet rei quaesitae, quoniam triplicatur proportio. 18 Atque ideo nunc radix cubica numeri 125 scilicet 5 sumitur pro precio rei. Sicut autem hic pro dignitatibus per quincuplam proportionem procedentibus, ita et pro aliis per duplam, triplam, quadruplam et aliam quamvis multiplicem multiplicem³³ dispositis faciam. Atque³⁴ haec est demonstratio primae regulae.

Secunda Regula

19 Cum ex tribus dignitatibus aequalitas fit inter congeriem minimae et mediae, et inter maximam: tunc cape 1/2 mediae³⁵. 20 Et talis dimidii quadratum coniunge cum minima. Et aggregati radicem iunge cum dimidio predicto. Et conflabis precium rei, cum dignitates sunt collaterales; vel quadratum talis precii, si dignitates distent per singulas medias; vel cubum precii, si per binas.

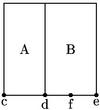
21 [a:20v] Exempli gratia, A 10³⁶ numerus cum B 3 rebus aequivaleat censui AB quod est quadratum³⁷. Quaero precium rei. Sit res ce latus scilicet census AB. Sitque³⁸ de rerum numerus datus. Eius 1/2 df vel fe scilicet³⁹ 11/2; huius 1/2 quadratum 21/4. Hoc cum A 10 numero facit 12 1/4. Huius radix cf 31/2, quae cum fe 1/2 dicto, conflat totum ce⁴⁰ 5 precium rei⁴¹.

22 Nam per 6^am Secundi Elementorum

cf  121/4 aequiperat

ec cd scilicet A 10  df scilicet 21/4

Sic demonstratur secunda regula. Quando scilicet tres dignitates fuerint collaterales. Si distent per singulas medias⁴² habebis quadratum quaesitae rei. Si distent per binas, habebis⁴³ cubum. Sicut ratio proportionum requirit⁴⁴.

Tertia Regula

[A:3v] 23 Cum ex tribus dignitatibus congeries minimae cum maxima fuerit aequalis mediae: tunc cape 1/2 mediae. Et ab eius quadrato aufer⁴⁵ minimam. Et residui⁴⁶ radicem iunge cum dicto dimidio et habebis precium rei. Vel a dicto 1/2 aufer⁴⁷ dictam radicem: et supererit precium rei. 24 Nam utroque modo, <uno⁴⁸> vel altero (ut postulat positio) satisfiet quaestioni, cum dignitates sunt collaterales. Vel supererit⁴⁹ quadratum talis precii, si dignitatibus intersint singulae mediae. Vel cubus ipsius precii, si binae mediae.

25 Exempli gratia, A 10 numerus cum B censu 1 aequivaleat Ab 7 res⁵⁰.

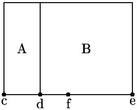
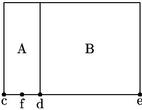
Sit cd latus unum numeri, de latus census in prima descriptione. At cf 31/2 dimidium rerum. Huius quadratum 121/4. Hinc demo 10 scilicet⁵¹ A numerum et supersunt 21/4 ; huius radix df 11/2 quae cum fe dimidio dicto scilicet⁵² 31/2 facit 5, quod est⁵³ precium rei. 26 Vel ab ipso 31/2 (sicut in altera figuratione) demo df 11/2 et relinquitur cd, 2⁵⁴ precium rei.

Nam per 5^am Secundi Elementorum

cf 121/4 aequivalet

cd de scilicet A 10  df scilicet 21/4

Sic demonstratur tertia regula, cum scilicet tres dignitates fuerint collaterales. 27 Quod si distent per singulas medias habes quadratum rei. Si vero per binas cubum. Ita enim postulat ratio proportionum⁵⁵.

Nunc veniemus ad quartam regulam.⁵⁶

[A:4r] [a:21r] Quarta Regula

Quando ex 3 dignitatibus cumulus mediae ac maximae adaequaverit minimam: tunc cape 1/2 mediae; cuius quadratum coniunge cum minima. Et ab aggregati radice deme dimidium mediae predictum. Nam supererit precium rei, si dignitates sint collaterales. 28 Vel quadratum talis precii, si dignitates⁵⁷ desgregentur per singulas medias. Vel cubus precii, si per binas.

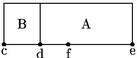
Exempli gratia: A 4 res cum B censu 1 adaequentur ipsi ab numero 45. Quaeritur precium rei. 29 Sit cd numerus rerum de latus census hoc est res ipsa. Et cf dimidium rerum scilicet⁵⁸ 2. Huius quadratum 4 quod cum 45 numero facit 49. Cuius radix 7 scilicet ef⁵⁹; hinc demo 2 dimidium predictum⁶⁰ et supersunt 5 scilicet de precium rei.

30 Nam per 6^am 2ⁱ Elementorum

ef scilicet61 49 conflat

ce cd scilicet 45   df scilicet 4

Sic demonstratur quarta regula, cum scilicet 3 dignitates extiterint collaterales. Quod si intercipiant singulas medias, habes quadratum rei. Si binas, cubum ob rationem in primam regulam assignatam et in caeteris⁶² commemoratam.

31 Oportet autem ut in dignitatum aequalitate census redigatur ad unitatem quo regula procedat per demonstrationes et calculum⁶³. Quod enim hic demonstratur in numero, re, ac censu per lineam, aream⁶⁴, et quadratum, ex 5^a et 6^a 2ⁱ Elementorum, verificatur de omnibus quantitatibus proportionalibus, per numerarios terminos assignatis. 32 Quem ad modum quidquid demonstratur in 2^o, 5^o, 7^o, 8^o, 9^o ac 10^o Elementorum libris de lineis et [A:4v] areis ac numeris⁶⁵, idem concluditur de omnibus per numerarios terminos assignatis quantitatibus sicut nos in Secundo Arithmeticorum latius docuimus. Nunc exempla singulis regulis applicabimus⁶⁶.

[a:21v] Exempla primae regulae

33 Est numerus quidam, cuius quadratus est 2/3 sui cubi: quaeritur. Ponatur numerus ipse⁶⁷ 1 res. Eritque eius quadratum 1 census, atque cubus 1 cubus. Quare, iuxta hypothesim 2/3 cubi adaequant 1 censum. Hoc est sunt 2 dignitates aequales. Itaque, per primam regulam, partior census per cubos, hoc est, partior 1 per 2/3 et proveniunt 11/2 precium scilicet rei, et numerus quaesitus, quoniam dignitates sunt collaterales⁶⁸. 34 Et convenit suppositioni⁶⁹. Nam huius numeri 11/2 quadratus scilicet 21/4 est 2/3 sui cubi scilicet 33/8.

Quaero⁷⁰ numerum, qui 4/9 habet sui cubi. Ponatur talis numerus 1 res eritque cubus eius 1 cubus. Atque ideo per hypothesim 4/9 cubi aequant 1 rem. 35 Per regulam ergo primam, partior res per cubos, hoc est partior 1 per 4/9 et prodeunt 21/4. Et hoc est⁷¹ quadratum precii rei⁷², quoniam dignitates distant per unam mediam. Igitur radix quadrata huius numeri 21/4 hoc est 11/2 fit precium rei. Et talis est quaesitus numerus qui iam habet 4/9 sui cubi qui est 33/8.

36 Sunt duo numeri quorum alter ad alterum duplus, productum autem minoris in quadratum maioris est 108: [A:5r] quaero singulos. Pono minorem 1 rem. Quare maior erit duae res. Eius quadratum 4 census. Unde productum illius in hoc quadratum erit 4 cubi. Igitur per hypothesim 4 cubi aequabunt 108. Et idcirco per regulam primam, partior 108 per 4 et proveniunt 27. 37 Et hic erit cubus precii rei quaesiti, quoniam dignitates distant per medias binas⁷³. Ergo radix cubica huius numeri⁷⁴ 27 hoc est 3, erit precium rei. Et tantus est minor numerus. Quare maior erit 6 quia duplus. Et iam 3 multiplicans 36 facit 108.

Exempla secundae regulae

38 Numerus quidam coniunctus cum 42 conflat suum quadratum: quaeritur. Ponatur 1 res: eius quadratum erit 1 census. Igitur 1 res cum 42 adaequant 1 censum⁷⁵. Ita ex tribus dignitatibus collateralibus, numero, re, censu mini[a:22r]ma cum media aequivalent maximae. 39 Quare, per secundam regulam, sumo quadratum 1/2 rerum scilicet 1/4 cui iungo 42 numerum et conficio 421/4, cuius radix quadrata 61/2; cui iungo 1/2 rerum scilicet 1/2 et conficio 7 et hoc est precium rei, quoniam dignitates erant collaterales. Igitur quaesitus numerus est⁷⁶ 7 qui iam coniunctus cum 42 conflat⁷⁷ 49 suum quadratum.

40 Quaeritur numerus cuius quadratum cum 72 coniunctus constituit⁷⁸ suum secundum quadratum. Ponatur 1 res eritque suum⁷⁹ quadratum⁸⁰ 1 census; secundum vero quadratum unus census secundus. Itaque 72 cum 1 censu [A:5v] aequivalent 1 censum secundum. Quare ex 3 dignitatibus, numero, censu, ac censu secundo aequidistantibus minima cum media aequiperant maximam. 41 Et ideo per regulam secundam capio dimidium mediae scilicet 1/2 eiusque quadratum 1/4 quod iunctum cum numero 72 facit 721/4 cuius radix quadrata est⁸¹ 81/2. Cui iungo dimidium mediae predictum scilicet 1/2⁸² et conficio⁸³ 9 quod est quadratum precii quaesiti, quoniam dignitates distant per singulas medias. Radix ergo quadrata⁸⁴ talis numeri hoc est 3 est precium rei. Cuius iam quadratum 9 iunctum cum 72 conflat 81 secundum quadratum rei eiusdem.

42 Quidam numerus, cuius cubus cum 702 coniunctus conflat quadratum sui cubi, quaeritur. Ponatur 1 res eius cubus erit 1 cubus Igitur quadratum sui cubi erit 1 census cubi. Itaque per hypothesim 702 numerus cum uno cubo adaequant 1 censum cubi. Quare ex 3 dignitatibus aequidistantibus minima cum media adaequant maximam. 43 Et idcirco sequens preceptum secundae regulae, capio dimidium mediae, scilicet 1/2, cuius quadratum 1/4 iungo cum minima, scilicet cum numero 702⁸⁵ et conficio⁸⁶ 7021/4. Cuius radix quadrata 261/2. Cui iungo dimidium mediae dictum, scilicet 1/2 et conflo⁸⁷ 27 cubus scilicet precii quaesiti⁸⁸, quoniam dignitates distant per binas medias. 44 Radix ergo cuba talis numeri, hoc est 3 erit precium quaesitum rei. Iam enim eius cubus 27 coniunctus cum 702 consummat 729 [A:6r] quod est quadratum sui cubi, sicut positio postulat.

[a:22v] Exempla tertiae regulae

45 Sunt duo numeri, quorum congeries 13, productum autem⁸⁹ 36: quaero singulos. Ponatur unus 1 res. Ergo reliquus erit⁹⁰ 13 minus 1 re. Duco hoc in illud, et produco 13 res minus 1 censu; hoc ergo productum⁹¹ per hypothesim aequiperat 36. Appono utrobique 1 censum et erunt 13 res aequales 36 numero cum 1 censu. 46 Ita ex 3 dignitatibus collateralibus minima cum⁹² maxima aequivalent mediam. Quare per tertiam regulam, capio dimidium mediae scilicet 61/2, cuius quadratum 421/4. Hinc demo minimam scilicet 36 et supersunt 61/4; cuius radicem scilicet 21/2 iungo cum dicto dimidio scilicet cum⁹³ 61/2 et conflantur 9 precium scilicet rei, quoniam dignitates sunt collaterales. 47 Et⁹⁴ tantus est unus ex quaesitis numeris. Igitur reliquus 4, quoniam amborum summa fuit 13⁹⁵. Estque iam eorum productum 36 sicut hypothesis vult⁹⁶. Vel dictam radicem 21/2 aufero⁹⁷ a dicto dimidio 61/2 et supersunt 4 pro precio rei, qui est unus quaesitorum numerorum. Unde, reliquus erit 9. Et utroque modo satisfit quaestioni. 48 Aliquando eligitur unus tantum modus, conveniens supposito.

Est numerus, cuius secundus quadratus coniunctus cum 18 conflat undecuplum sui quadrati: quaeritur. Ponatur 1 res. Eius quadratus ⁹⁸ 1 census. At secundus quadratus erit⁹⁹ 1 census secundus¹⁰⁰. Ita iuxta hypothesim 1 census secundus¹⁰¹ cum 18 aequiperant 11 census. Sic ex 3 dignitatibus aequidistantibus, minima et maxima aequiperant mediam. 49 Ergo per tertiam regulam capio dimidium mediae scilicet 51/2, cuius quadratum 301/4; hinc aufero¹⁰² minimam 18 et supersunt 121/4 cuius radix 31/2 [A:6v] coniuncta cum dicto dimidio, scilicet cum¹⁰³ 51/2, (nam subtracta non respondet¹⁰⁴) ^[1] conflat 9, quod est quadratum precii rei, quoniam dignitates distant per singulas medias. 50 Igitur radix 9 hoc est 3 fit precium rei quaesitum. Cuius iam secundum quadratum scilicet 81 cum 18 conflat 99, quod est undecuplum quadrati precii scilicet 9¹⁰⁵, sicut quaestio supponit. Quin¹⁰⁶ etiam si 31/2 auferres a dicto dimidio 51/2, superesset 2 quod potest esse quadratum precii rei; et ipsa res radix 2. Nam 4 (quod est secundum eius quadratum) iunctum cum 18 conflat 22, quod est undecuplum ad 2 quadratum primum.

51 Numerus quidam, cuius cubi quadratum cum 81 conflat sui cubi trigecuplum: quaeritur. Ponatur 1 res. quadratum sui cubi erit 1 census cubus. Eius autem cubus 1 cubus. Ita per hypothesim iam 1 census cubus cum 81 numero adaequant 30 cubos. Quare ex 3 dignitatibus aequidistantibus minima cum¹⁰⁷ maxima adaequant mediam. 52 Ergo per tertiam regulam, capio 1/2 mediae scilicet 15 cuius quadratum 225; hinc demo minimam scilicet 81 et restant¹⁰⁸ 144. [a:23r] Cuius radix 12 iuncta cum antedicto¹⁰⁹ 1/2 scilicet cum¹¹⁰ 15 facit 27¹¹¹ et hic est cubus precii rei, quoniam dignitates distant per binas intermedias. 53 Igitur radix cuba 27 hoc est 3 fuit precium rei quaesitum. Iam enim quadratum eius cubi scilicet 729 cum 81 conflat 810, quod est trigecuplum cubi¹¹². Vel¹¹³ 12 auferatur a dimidio dicti 15 et superest 3 et similiter radix cuba 3 potest esse precium rei. Nam quadratum huius cubi 3 scilicet 9 iunctum cum 81 facit 90 trigecuplum cubi ut prius.

Exempla quartae regulae

54 Duo numeri, quorum differentia 3 et quorum productum 40 quaeruntur. Ponatur minor 1 res. Igitur reliquus [A:7r] erit 1 res cum 3. Duco hoc in illud, et produco 1 censum cum 3 rebus, quod per hypothesim adaequat 40. Ita ex tribus dignitatibus collateralibus, media et maxima adaequant¹¹⁴ minimam. Itaque per¹¹⁵ quartam regulam capio dimidium mediae scilicet 11/2, cuius quadratum 21/4; quod iungo cum minima scilicet¹¹⁶ 40 et fiunt¹¹⁷ 421/4, a cuius radice 61/2 demo dictum 1/2 mediae, scilicet 11/2 et supersunt¹¹⁸ 5 precium scilicet rei quaesitum, quoniam dignitates sunt collaterales. 55 Minor ergo numerus 5; quare maior fiet¹¹⁹ 8, quorum productum 40 sicut quaestio supponit¹²⁰.

Numerus quidam, cuius quatuor quadrata cum secundo eius quadrata conflant 117 quaeritur. Ponatur 1 res; eius quadratum 1 census. Secundum autem quadratum 1 census secundus¹²¹. Ergo per hypothesim 4 census cum 1 censu secundo¹²² aequivalent 117. 56 Unde ex tribus dignitatibus aequidistantibus nunc media et maxima aequant minimam. Itaque per¹²³ regulam quartam capio 1/2 mediae scilicet 2, cuius quadratum 4 iungo cum minima 117 et conficio 121. Ab huius radice 11 subtraho dictum dimidium scilicet¹²⁴ 2 et supersunt¹²⁵ 9 quadratum scilicet precii rei, quoniam dignitates distant per singulas medias. Ergo radix 9 hoc est 3 est precium rei. Cuius iam quatuor quadrata scilicet 36 cum secundo eius quadrata scilicet 81 conficiunt 117, sicut quaestio supponit.

57 Quaeritur numerus, cuius cubus cum quadrata sui cubi conflat 4160. Ponatur 1 res eritque cubus eius 1 cubus; quadratus autem cubi erit 1 census cubicus¹²⁶ Ergo per hypothesim, 1 cubus cum 1 censu cubico aequiperant numerum 4160. Unde ex tribus dignitatibus aequaliter distantibus, media cum maxima aequivalet minimam¹²⁷. 58 Ergo per¹²⁸ quartam regulam sumo 1/2¹²⁹ mediae scilicet 1/2, cuius quadratum 1/4 [a:23v] iunctum¹³⁰ minimae scilicet 4160 conficit 41601/4, cuius radix 641/2. Hinc demo dimi[A:7v]dium predictum scilicet 1/2 et remanent¹³¹ 64. Igitur radix cubica¹³² 64 hoc est 4 est precium rei, quoniam dignitates distant per binas intermedias. 59 Iam enim eius cubus 64¹³³ cum quadrata cubi, quod est¹³⁴ 4096 coniunctus conflat 4160, sicut a quaerente¹³⁵ supponitur.

Quoniam autem dignitates tres, quarum fit collatio, removentur per ternas intermedias, tunc inventum erit secundus quadratus precii quaesiti. 60 Quare precium rei erit radix secunda illius¹³⁶. Sic per quatuor regulas satisfit infinitis quaestionibus. Non solum circa numeros sed etiam circa lineas, areas et solida et omnimodas magnitudines¹³⁷. Quas perspicacia lectoris formare¹³⁸ et [et¹³⁹] accommodare poterit ad exercitium ingenii¹⁴⁰.

61 Utitur autem regulis algebrae Io. de monte Regio ad confutanda sophismata Nicolai Cusae de circuli quadratura scribentis. Utitur et regula duarum falsarum positionum. Sed attendat tua perspicacia mi Cristofore Clavi¹⁴¹ (ut ego sentio et ex meis demonstrationibus constare potest) regulas algebrae non esse plures quam quatuor quamvis alii sex ponant. 62 Et etiam¹⁴² sub dictis quatuor comprehendi regulas infinitas¹⁴³ pro distantia dignitatum varia¹⁴⁴. Quae distantia¹⁴⁵ non variat regulam, quamvis faciat ut inventum quandoque sit ipsum rei precium quandoque radix quadrata et quandoque radix cubica aut radix quadrata secunda ipsius precii. Ex qua varietate aliqui multiplicant regulas.

Hactenus de algebra.