PROPOSITIO VII
39 Iisdem suppositis , et producta extrorsum collocata, potest a centro ad ipsam linea educi, ita ut pars eductae, inter peripheriam et collocatam compraehensa, ad partem tangentis inter contactum <et4> eductam, habeat rationem datam. 40 Oportebit autem datam rationem esse maiorem ea, quam habet dimidium collocatae ad sibi perpendicularem a centro.
41 In eadem descriptione, ponatur data ratio F ad G maior quam ratio CH ad HK, et ideo maior quam ratio KC ad CL. Sit ergo sicut F ad G, sic KC ad CX, eritque [S:200] CX minor quam CL.
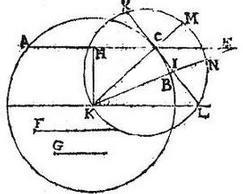
42 Describatur circulus per puncta L, K, X, et quoniam XC minor est quam CL, et utraque ad rectos ipsi KCM, ideo potest duci linea IN aequalis ipsi CM, quae producta cadat in punctum K, secans peripheriam ACB apud B, ipsamque AC productam apud E. 43 Eritque, per 33am tertii Elementorum 5, rectangulum XI, IL aequale rectangulo KI, IN, et quoniam propter similitudinem triangulorum KIL, EIC est sicut LI ad KI, sic LC ad KE. 44 Ideo, per 15<am> sexti, rectangulum LI, KE aequum est ipsi rectangulo KI, LC. Igitur sicut est rectangulum LI, KE ad rectangulum XI, IL, sic est, et rectangulum KI, LC ad rectangulum KI, IN. 45 Sed per primam sexti, sic etiam est linea KE ad lineam XI, et sic linea LC ad lineam IN, hoc est linea LC ad lineam CM. per 33am tertii Elementorum6 et per 15<am> sexti, sicut LC ad CM, sic iam KC ad CX, hoc est KB ad CX. 46 Igitur sicut KB ad CX, ablatum ad ablatum, sic erit iam, et KE ad XI, totum ad totum; quare, et sic erit EB ad CI residuum ad residuum, hoc est sicut F ad G. Et hoc iam possibile fieri demonstrandum erat.
47 Sequuntur alia duo lemmata circa magnitudinum progressionem.