PROPOSITIO XI.

Quod ante praemissa proposuit aliter demonstrare.

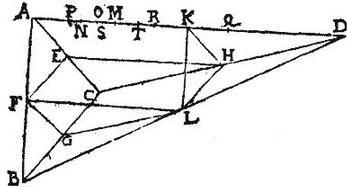
Repetens eandem descriptionem ex divisione pyramidis ABCD, sumemus pyramidem verticalem HKLD, et unam ex pyramidibus tribus ad basim, quae sit BGFL; reliquum vero dividemus in duo prismata serratilia, quorum unum bases triangulas habet AEF, HKL; alterum autem basim quadrilateram EFGC, quae serratilia per 40. XI. Euclidis, inter se aequalia sunt, et simul sumpta sunt triplum pyramidum BFGL, HKLD simul sumptarum; quandoquidem una, et utralibet dictarum pyramidum est pars octava pyramidis totalis; et ambae sunt simul quarta pars pyramidis totalis; itaque divisa ut antea per medium linea AK in puncto M. Demonstrandum est, quod centrum pyramidis ABCD est in plano basi [S:166] ABC parallelo ducto per M punctum: sit enim AN tertia pars ipsius AK, eritque MN sexta pars ipsius AK, secetur per medium MN in puncto O, cumque per 4. huius, centrum serratilis AEL sit in plano per punctum M: centrum autem serratilis EGH sit in plano per punctum N; atque serratilia sint aequalia: iam per 8. huius, commune centrum huiusmodi serratilium erit in plano per punctum O: (intelligendo semper plana aequidistantia basi ABC) posito autem centro totalis pyramidis ABCD in plano per punctum M: sectaque per medium AM in puncto P: erit per 7. postulatum, centrum pyramidis BFGL in plano per punctum P; sit ipsi AP aequalis KQ. Eritque centrum pyramidis HKLD in plano per punctum Q: secetur per medium PQ apud R; eritque commune centrum pyramidum dictarum in plano per punctum R, atque unaqueque linearum AP, PM, MR, RK, KQ fiet pars quarta ipsius AK: igitur RM tripla est ipsius MO: et triplum est aggregatum serratilium, cuius centrum in plano per punctum O, aggregati pyramidum, cuius centrum in plano per punctum R: convenit itaque per 8. huius, ut centrum totius scilicet pyramidis totalis ABCD sit in plano per punctum M.

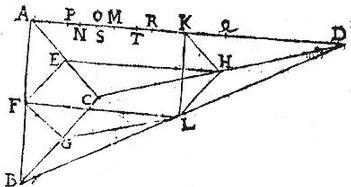
Alibi enim si ponatur, sequetur absurditas, ut si sit in plano per punctum O; cum in eodem plano sit commune centrum serratilium: erit per 7. primi, in eodem, et centrum commune pyramidum: quare punctum P cadet ultra punctum A, et ideo centrum pyramidis BFGL cadet extra ipsam pyramidem, quod est absurdum per ultimum postulatum. Idem a fortiori accidet, si centrum pyramidis totalis ponatur in plano per aliquod punctum inter puncta A, O; si autem ponatur a puncto O ad partes D, ut pote in plano per punctum S inter ipsa O, M puncta: tunc per 7. postulatum; puncta P, Q. tranferentur versus partes A per spatium dimidium ipsius MS, cum in similibus solidis centra similiter, hoc est proportionaliter sint disposita; et proinde punctum R, quod medium est ipsorum P, Q tantundem recedet ad partes A, hoc est per spatium dimidium ipsius MS, sit tale spatium RT: maius ergo erit spatium ST spatio MR. Itaque cum per centra partium, scilicet serratilium tamquam unius partis, et pyramidum tamquam alterius partis ducantur plana, quae per puncta O, T: atque per centrum totius scilicet pyramidis totalis ABCD, ducatur planum: quod per punctum S; sitque pars partis tripla, hoc est aggregatum serratilium triplum aggregati pyramidum: erit iam; per 8. huius, linea TS tripla ipsius SO: sed et tripla fuit RM ipsius MO, maior autem fuit TS ipsa MR triplum scilicet triplo; ergo et simplum simplo maius, ipsa videlicet SO, maior ipsa OM; pars toto: quod est absurdum: non ergo erit centrum pyramidis ABCD in plano per punctum S: similiter ostendetur non esse in ullo alio basi ABC parallelo plano, quam per punctum M ducto; sicut fuit demonstrandum.

Hinc ergo rursum quod decima proponit, demonstrari potest, sicut iam ex nona praecedenti demonstrata fuerat. [S:167]

Alia demonstratio eiusdem undecimae.

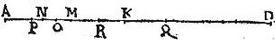
Rursum ex pyramide ABCD sumo eandem hypothemisam AD, sitque AM pars tertia residui MD; ductoque (ut in nona) plano: dico quod in tali plano erit centrum pyramidis: secetur enim pyramis ABCD ut in 11. in duo serratilia aequalia, duasque pyramides aequales ut ibi: et linea AD per aequalia apud K; unde et AK per aequalia apud M fiet; sed AN sit dimidium ipsius NK: unde PN fiet pars duodecima ipsius AK, et MN pars sexta eiusdem, qua per medium divisa apud O fiet unumquodque trium spatiorum PN, NO, OM pars duodecima totius AK. Item ipsi AP aequalis ponatur KQ, eritque PQ aequalis ipsi AK, et divisa PQ per aequa apud R, sic stabit ponderum ratio: nam centrum serratilis super basim trigonam erit in plano ducto per M; et centrum reliqui serratilis in plano per N per 4. huius. Centrum commune dictorum serratilium in plano per O per 16. primi, centrum pyramidis partialis ad basim in plano per P centrum pyramidis partialis ad verticem in plano per punctum Q per ultimum postulatum. Centrum commune talium pyramidum duarum in plano per¹ punctum R congruit itaque ponderum ratio supposito, quando serratilia inter se aequalia, et centrorum partialium a centro communi distantiae aequales; nec secus in pyramidibus partialibus: item centrum totalis pyramidis punctum M, et centra partium O, R, bene habent; nam una partium scilicet aggregatum serratilium tripla est ad reliquam scilicet ad aggregatum pyramidum, et spatium RM triplum ad spatium MO, quandoquidem MR aequalis ipsi PM: neque aliter se habere hanc centrorum dispositionem, possibile est: nam secus sicut in praemissa; sequetur impossibile contra 27. primi; ut scilicet spatia ponderibus reciproca esse nequeant. Constat ergo propositum.