PROPOSITIO IX.

Si pyramidis triangularis hypothemisa quaelibet, ita secetur, ut portio ad basim recepta sit tertia pars portionis ad verticem relictae: per punctum autem sectionis, ducatur planum basi aequidistans; ductum planum ibit per centrum gravitatis pyramidis.

Esto pyramis ABCD super basim triangulam ABC, habens verticem D, et quaevis hypothemisa a vertice ad basim, ut pote DA secetur apud M punctum, itaut AM portio sit pars tertia portionis MD, atque per M punctum ducatur planum aequidistans basi ABC: aio quod tale planum incedet per centrum gravitatis pyramidis ABCD: quod sic ostendo. Secentur pyramidis ABCD singula sex latera per medium in ipsis punctis E, F, G, H, K, L: quae puncta coniungantur ductis duodecim lineis in ipsis quatuor pyramidis basibus: sic enim relinquentur ad vertices pyramidis quatuor pyramides inter se aequales, et totali pyramidi similes: solidum autem in medio relictum erit octahedrum contentum sub octo triangulis; quarum bina quaeque opposita sunt alterum alteri aequidistantia, et aequilatera, et similia uni basium pyramidis: itaque planum aequidistans triangulo ABC ductum per punctum M, cum secet ipsam AK pe aequalia secabit singula octahedri latera, et axes per aequalia: et proinde ibit per communem sectionem axium octahedri: sed per praecedentem 7. huiusmodi communis sectio est centrum octahedri: ergo planum praedictum ibit per centrum octahedri: quod si tale planum non eat per centrum pyramidis ABCD, sit, si possibile est, centrum pyramidis in alio plano parallelo basi, et ducto per aliud punctum, quod sit N in hypothemisa AD: sit item centrum commune quatuor pyramidum partialium ad vertices relictarum in plano basi parallelo ducto per punctum O. Eritque per praecedentem, planum per N. Inter plana M, O puncta: quandoquidem planum per N ductum it per centrum totius pyramidis ABCD: plana vero per M, O puncta eunt per centra partium; quarum una est octahedrum, altera congeries quatuor pyramidum ad vertices relictarum: sit autem commune centrum trium pyrami[S:164]dum partialium super planum ABC positarum in plano parallelo ducto per P punctum. Et quoniam latus pyramidis magnae DA duplum est lateris AK pyramidis parvae: idcirco per 7. postulatum, duplex erit linea MA lineae AP: sit ipsi AP aequalis linea KQ. Eritque centrum pyramidis partialis ad verticem in plano basi parallelo per punctum Q ducto.

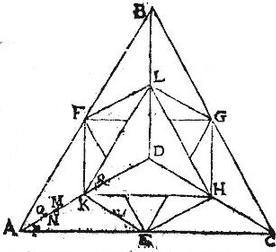
Itaque quoniam trium planorum aequidistantium per puncta O, P, Q ductorum, quod per punctum O ducitur, it per centrum totius, scilicet quatuor pyramidum partialium: quod autem per punctum P it per centrum unius partium, scilicet per centrum trium pyramidum super ABC positarum: quodque per punctum Q it per centrum reliquae partis scilicet pyramidis ad verticem: idcirco per precedentem, horum planorum medium erit quod per punctum O: et quoniam una partium tripla est ad reliquam, hoc est congeries trium pyramidum ad basim ad pyramidem verticis: ideo per praemissam, linea QO tripla ipsius OP. Igitur OP quarta pars ipsius PQ, et perinde quarta pars ipsius AK, et ob id dimidium ipsius AM: fuit autem PN dimidium ipsius NA: maius autem MA ipso AN duplum duplo: maius ergo dimidium dimidio, hoc est maior linea OP ipsa linea PN: pars toto: quod est impossibile: non est igitur centrum pyramidis ABCD in plano basi parallelo per punctum N: et similiter arguetur quod in nullo alio basi ABC parallelo plano, quam per punctum M ducto, existet; et hoc proponebatur demonstrandum. Alia demonstratio eiusdem nonae.

Ex pyramide ABCD sumo hypothemisam AD, quae secetur in puncto M, itaut AM sit pars tertia ipsius MD, et per punctum M ducatur planum parallelum basi ABC: dico quod in tali plano erit centrum pyramidis ABCD; secetur enim, ut in nona, pyramis ABCD in quatuor pyramides invicem similes, et aequales, relicto octahedro pyramidibus contiguo, ut ibi: et secetur linea AD per aequalia apud K: et rursus AK per aequa apud M: demum AM per aequa apud P: itaque AP erit pars tertia ipsius PK: sit ergo et KQ pars tertia ipsius QD; eruntque AP, KQ aequales: eritque per penultimum, et ultimum postulatum, centrum commune trium pyramidum partialium ad basim in plano basi parallelo per punctum P, et centrum pyramidis ad verticem in plano per punctum Q: quare centrum commune talium quatuor pyramidum erit in plano per punctum M per 27. primi, cum tres pyramides basis sint triplum pyramidis ad verticem; et spatium MQ triplum spatii PM: centrum autem relicti octahedri in plano per punctum M per 7. quarti: congruit itaque ratio ponderum supposito. Non enim aliter se habere centra possibile est: sit enim totalis ABCD pyramis centrum in plano per punctum N, et tunc per dictum postu[S:165]latum, erit in plano per punctum O (itaut MO pars sit ipsius MN spatii) sit ipsarum quatuor partialium pyramidum centrum, cum dimidia sint earum latera laterum pyramidis totalis: sed per 7. huius, centrum octahedri relicti fuit iam in plano per punctum M: igitur N centrum totius non statuetur in medio ipsorum M, O centrorum, quae sunt centra partium: quod est absurdum: constat ergo propositum.