PROPOSITIO XVI.

Si in duabus conicis sectionibus, quae vocantur parabolae inscribantur perspecte duo eiusdem numeri laterum rectilinea easdem cum sectionibus bases habentia talia rectilinea componentur ex singulis ad verticem triangulis, et ex eiusdem numeri trapetiis aequidistantium laterum, in quibus correlativa latera aequidistantia erunt proportionalia, et correlativi axes proportionales, et axes rectilineorum totales per medium secabunt singula aequidistantium laterum.

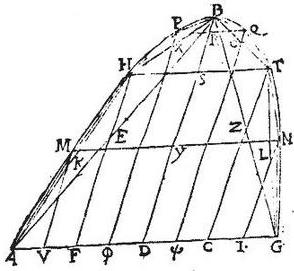
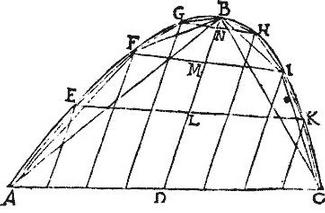
Sint duae parabolae ABC, XOP, in quibus inscribantur singula rectilinea novem laterum, ut in praecedenti dictum est, habentia easdem bases cum parabolis, quae sint AEFGBHIKC, cuius axis BD: atque XLYQOZVTP, cuius axis OR; et coniungantur GH, FI, EK, quae per praecedentem, aequidistabunt basi AC. Item coniungantur QZ, YV, LT, quae similiter aequidistabunt basi XP. Dico igitur, quod huiusmodi rectilinea constabunt ex singulis triangulis GBH, QOZ ad vertices, et ex ternis trapetiis, scilicet FGHI, EFIK, AEKC, et reliquum ex ipsis YQVZ, LYVT, XLTP, in quibus correlativa latera aequidistantia erunt proportionalia, hoc est GH ad QZ, et FI ad YV, et EK ad LT, et AC ad XP, eandem proportionem habebunt, et axes correlativi proportionales, hoc est BN ad OS, et [S:147] NM ad S, et ML ad X, et LD ad XR, eandem rationem habebunt; quod ex praecedenti constat, nam ut est ostensum, proportio aequidistantium est sicut numerorum ab unitate ordinatorum naturali ordine procedentium, et proportio axium est sicut numerorum imparium ab unitate ordinatorum in omni tali rectilineo perspecte in quavis parabola inscripto; item axes bifariam secabunt singulas aequidistantes.

Quippe quae demonstranda proponuntur.