F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber secundus 4
<- App. -> <- = ->

PROPOSITIO IV.

Centrum parallelogrammi est in sectione diametrorum.

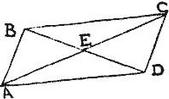
figura 6

Esto parallelogrammum ABCD, cuius diametri AC, BD se vicissim secent in puncto E: aio quod E punctum est centrum gravitatis parallelogrammi: nam propter aequidistantiam linearum triangulum AEB aequiangulum est triangulo CED: et per 34. primi Euclidis, latus CD aequum lateri AB: igitur triangulum AEB aequilaterum triangulo CED per 26. eiusdem; itaque latus CE aequale lateri EA: et perinde diameter AC per aequalia secatur in puncto E: per praecedentem ergo punctum E centrum gravitatis parallelogrammi ABC est: quod fuit demonstrandum.

Inizio della pagina
 ->