DE MOMENTIS AEQUALIBUS
Propositionum, quarum quaedam sunt theoremata, quaedam problemata.
PROPOSITIO PRIMA.
Centrum gravitatis circuli est idem quod, et magnitudinis.
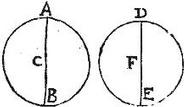
In circulo AB centrum gravitatis sit punctum C: aio quod C punctum est ipsum circuli AB centrum: exponatur enim ipsi AB circulo aequalis circulus DE, in quo centrum gravitatis sit F: et per ipsa C, F puncta ducantur circulorum diametri AB, DE, quae aequales erunt, quandoquidem aequales sunt circuli: coaptetur igitur circulus DE circulo AB, itaut diameter DE diametro AB congruat. Tunc enim, quoniam per sex postulatum, congruentium figurarum congruunt centra gravitatum: congruet iam punctum F puncto C, et linea DF lineae AC, et linea FE lineae CB congruet: commutatis autem diametrorum extremis, itaut superiora inferioribus congruant, hoc est, ut punctum D puncto B, atque punctum E puncto A conveniat, ac rursum circulus circulo coaptetur: rursum iam per sex postulatum, congruet centrum F centro C, et linea DF lineae CB conveniet, et reliqua reliquae: itaque linea DF, quae congruebat in prima circulorum coaptatione, lineae AC nunc in secunda congruit lineae CB: aequales ergo sunt lineae AC, CB, ut quae mensurantur ab eadem linea DF: et perinde cum diameter sit AB, erit C punctum centrum circuli AB: quod erat demonstrandum.
Idem aliter demonstratur sic: coaptetur circulus DE circulo AB itaut diameter DE diametrum AB secet; et quoniam per sex postulatum, congruentium figurarum gravitatum centra, congruet iam centrum gravitatis F centro gravitati C, et propterea diametri secabunt se vicissim super puncto C, suntque diametri AB, DE eiusdem circuli, quandoquidem congruentibus periferiis, unus fit circulus; diametri autem secant se super centro: igitur C centrum magnitudinis est circuli AB: sicut proponitur demonstrandum.