F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber primus 25
<- App. -> <- = ->

PROPOSITIO XXV.

Centrum gravis uniformis est in facta per medium axis sectione.

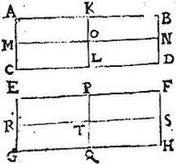
figura 23

Uniforme grave appello, quod est aequidistantium laterum, sive illud sit parallelogrammum planum, sive solidum parallelepipedum: axim autem rectam; quae lateribus aequidistans per centrum gravitatis incedit. Sit itaque grave parallelogrammum ABCD, in quo centrum gravitatis sit O: et per ipsum O punctum agantur lateribus aequidistantes rectae KL, MN, quarum utraque axis vocabitur parallelogrammi: dico igitur quod tam KL axis quam MN axis per aequalia secantur in puncto O, quod sic ostenditur. Describatur ipsi ABCD parallelogrammo aequilaterum, et aequiangulum parallelogrammum EFHG, in quo centrum gravitatis per 5. huius, compertum sit T; per quod axes ducti sunt PQ, RS: deinde coaptetur parallelogrammum EH parallelogrammo AD, ut latus EF lateri AB, et latus EG lateri AC congruat, et reliqua reliquis: sic enim per 6. postulatum, centrum gravitatis T, centro gravitatis O congruet, et axis PQ axi KL, et axis RS axi MN propter aequidistantiam linearum conveniet. Itaque linea PT lineae KO, et linea TQ lineae OL congruet; commutatis autem lateribus, ut superiora inferioribus coaptentur, hoc est, ut EF ipsi CD, et GH ipsi AB congruat: iam linea TP lineae OL, et linea [S:98] QT lineae KO congruet, quandoquidem per 6. postulatum, centra gravitatum T, O rursum congruent, coaptatis rursum gravibus.

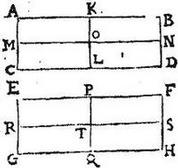
figura 24

Itaque quoniam linea PT nunc lineae KO nunc ipsi OL congruit, iam idcirco aequales erunt KO, OL; similiter commutatis lateribus, ut dextra sinistris coaptentur; hoc est ut EG ipsi BD, atque FH ipsi AC congruat (congruentibus semper gravitatum centris O, T per 6. postulatum) iam linea RT, quae lineae MO congruebat, iam ipsi ON congruet, et perinde aequales erunt MO, ON; igitur ipsius gravis AD uniformis centrum gravitatis O est in facta per medium sectione tam axis KL, quam axis MN: quod fuit demonstrandum. Sed in solido parallelepipedo addetur tertius axis ob triplicem dimensionem solidi; et similiter demonstrabitur in solido parallelepipedo centrum gravitatis esse in eo puncto, in quo per aequalia se intersecant tres axes singuli singulos.

Inizio della pagina
 ->