PROPOSITIO XVI.

Centra gravium aequalium aequaliter distant a communi centro.

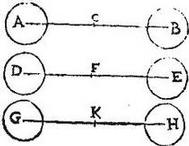
Hoc est centra partium aequalium aequaliter distent a centro totius. Ut si sint duo gravia aequalia A, B: quorum centra A, B, et quorum tanquam unius commune centrum C. Aio quod spatia AC, CB sunt aequalia. Sint enim duo gravia D, E ipsis A, B gravibus aequalia, quorum centra D, E, et quorum tamquam unius commune centrum F; sitque linea DE lineae AB aequalis: rursum sint duo gravia G, H praedictis aequalia, quorum centra G, H, et quorum tanquam unius commune centrum K, et linea GH lineae DE aequalis; sitque utrumque gravium G, H utrique gravium D, E simile, et aequale, similiterque positum, itaut coaptatis lineis DE, GH, hoc est congruentibus gravitatum centris D, G: nec non congruentibus gravitatum centris E, H; congruant gravia D, G, itemque congruant gravia E, H; et vicissim commutatis centris, hoc est coaptatis centris D, H simul, centrisque E, G simul, ut congruant rursum gravia D, H, et deinde gravia E, G: itaque fiet per 6. postulatum ut coaptatis gravibus congruant semper centra F, K: quamobrem in prima coaptatione linea GK congruet lineae DF; et in secunda coaptatione linea GK congruet lineae FE, et perinde aequales erunt lineae DF, FE, ut quae mensurentur ab eadem linea; et similiter lineae GK, KH aequales erunt: verum per x. huius gravia A, B aequeponderant a puncto C; et gravia D, E aequeponderant a puncto F, et haec illis singula singulis aequalia, et ad idem intervallum AB, DE posita: igitur per 12. huius horum centra a communi centro, et illorum centra a communi centro ad easdem absunt distantias, hoc est linea AC aequalis ipsi DF, et linea CB aequalis ipsi FE: sed aequales fuerunt DF, FE: igitur et aequales erunt AC, CB: quod fuit demonstrandum.