PROPOSITIO VII

27 Aggregatum eorum, quae fiunt ex utraque chordarum duorum arcuum inaequalium in chordam residui de semicirculo alterius, rectangulorum ad differentiam eorundem est sicut chorda aggregati ex eisdem arcubus ad chordam arcus differentiae eorundem.

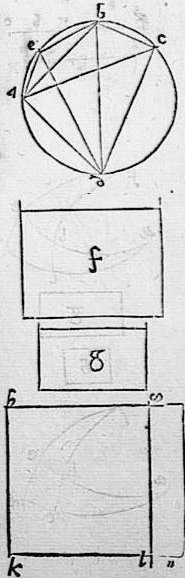
28 In circulo abc sunto duae chordae ab bc quarum maior ab et posita ipsi bc aequali be. Ducatur chorda ea ductaque diametro circuli bd, ducantur chordae ad dc ca. Eritque ac chorda aggregati ex arcubus ab bc atque ae chorda differentiae eorundem. Itaque ex ab in cd vel ed fiat quadrangulum f et ex bc sive be in ipsam ad fiat quadrangulum g. 29 Iam demonstrandum est quod: aggregatum ex quadrangulis f g habet ad eorundem differentiam talem rationem qualem habet chorda ac ad chordam ae. 30 Exponatur enim ipsi bd aequalis linea hk, super quam constituatur rectangulis f g aequale quadrangulum hklm et ipsi lm applicetur quadrangulum mn aequale differentiae ipsorum quadrangulorum f g. 31 Cum autem per praecedentem, totum quadrangula f g sit aequale quadrangulo quod ex bd ac, erit iam quadrangulum km aequale quadrangulo quod ex bd ac. Sed hk aequalis ipsi bd, ergo kl aequalis ipsi ac. 32 Item cum ex praecedenti, quadrangulum f quod iam fit ex ab ed sit aequale quadrangulo g quod iam fit ex be ad una cum quadrangulo quod ex ae bd atque ob id quadrangulum ae bd sit ipsorum quadrangulorum f g differentia, ideo ipsum quadrangulum mn aequum ipsi differentiae aequale erit quadrangulo ae bd. Sed lm aequalis ipsi bd, ergo similiter et ln aequalis ipsi ae. 33 Per primam autem sexti Euclidis, quadrangulum km ad quadrangulum mn sicut kl ad ln; igitur et aggregatum quadrangulorum f g ad differentiam eorum sicut kl ad ln hoc est sicut chorda ac ad chordam¹⁵ ae. Quod erat demonstrandum.