THEOREMA XXX

99 Si in cavum speculum a puncto quopiam tres radii incidant, unus quidem per centrum, duo vero a centro aequaliter distantes, hi ad signum unum concurrent³⁴⁵, quod in radio, qui per centrum.

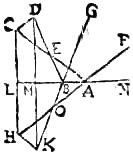
100 In cavum speculum AB a signo C cadant³⁴⁶ radii CD quidem per centrum speculi E, at³⁴⁷ CF et CG aeque³⁴⁸ a centro E remoti³⁴⁹. Dico quod CF et CG radii reflexi ad signum unum concurrent in radio CD. Reflectatur enim³⁵⁰ CF ad CD in signo H, et connectantur³⁵¹ H, G³⁵². Et quoniam CF, CG aeque³⁵³ removentur a centro, ideo³⁵⁴[C:21r] anguli CFA, CGB sunt invicem aequales. Sed CFA est aequalis ipsi HFD³⁵⁵ per 27. Ergo angulus CGB aequalis est ipsi HFD. Sed propter aequales arcus FD et DG, ipse³⁵⁶ HFD angulus aequalis est ipsi HGD. Ergo CGB angulus est³⁵⁷ aequalis ipsi HGD. Per 27 ergo³⁵⁸ ipse radius CG in signum H reflectitur. Ipsi er[S:25]go <radii³⁵⁹> FH, GH reflexi ad signum H, in signo radii CD concurrunt.

Corollarium

101 Si ergo in cavum speculum³⁶⁰ a puncto quopiam per centrum radius incidat, ac posito polo³⁶¹ puncto casus in superficie speculi circulus describatur, quicumque radii ab eodem signo ad eius circuli peripheriam ceciderint, omnes ad unum punctum in radio, qui per centrum, concurrent. Patet, nam tales radii aequaliter a speculi centro removentur³⁶², quandoquidem a puncto in axe circuli ad ipsius circuli periferiam delabuntur, atque ideo cum axe et circuli semidiametro aequilatera facient triangula³⁶³.³⁶⁴