[S:21]

THEOREMA XXVII

87 Obliquus in speculum radius ad aequalem inclinationis angulum in plano ad speculum recto reflectitur.

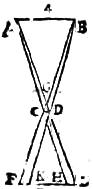
88 Sit enim speculum AB, in quod obliquus radius CD cadat, qui reflectatur in E. Aio quod aequalis est angulus ADC²⁶⁸ inclinationis angulo reflexionis²⁶⁹ BDE²⁷⁰, quodque²⁷¹ CD et DE sunt in plano super speculum orthogonaliter erecto²⁷². Si enim ipsis CD et DE in plano ad speculum recto consistentibus ipse²⁷³ ADC angulus non sit ipsi BDE²⁷⁴ angulo aequalis, sit maior. Radius ergo obliquus ad maiorem semper inclinationis angulum incidet quam reflectetur²⁷⁵. Transferatur ergo C signum radians in signum E illuminatum, ipsum vero E in C. Et radiabit adhuc E in C per EDC tramitem, quarto supposito volente. Maior itaque erit BDE²⁷⁶ angulus[C:18r] ipso²⁷⁷ ADC. Fuerat autem minor, quod est impossibile. Non est ergo ADC angulus ipso BDE maior. Similiter ostendemus quod nec minor, igitur aequalis. Ponatur²⁷⁸ autem quod planum, in quo AB et CD lineae, sit speculo rectum. Iam et ipsa DE in eodem est plano. Si enim extra, ducatur²⁷⁹ ergo DF ad speculum inclinata, sicut DE, atque angulo FDC ipsi EDC aequali existente (hoc enim possibile est) eritque ut sicut CD in E, sic etiam in F reflectatur²⁸⁰, quod est absurdum per tertium suppositum. Astruitur ergo quod propositum est.

Corollaria²⁸¹

89 1²⁸² Ex praemissis sequitur, ut ex secundaria²⁸³ luce, quae tam ab illuminatis a sole superficiebus quam a planis speculis reflectitur, secundarius quoque calor generetur, atque adeo ex reflexione²⁸⁴ solaris calor²⁸⁵ accrescat.

90 2²⁸⁶ Satis ergo liquet quod tam in convexis quam in cavis speculis reflexio fit in plano per ipsius speculi centrum, radiis aequales facientibus angulos²⁸⁷ cum periferia circuli, qui plani per centrum et specularis superficiei communis est sectio. In²⁸⁸ speculis autem cylindricis²⁸⁹, tam convexis²⁹⁰ quam cavis²⁹¹, reflexio fit in plano[C:18v] utcumque²⁹² cylindrum secante, radiis, ad terminum diametri cylindricae qui in plano secante est, coeuntibus et aequales angulos continentibus cum linea, quae communis est sectio secantis plani et cylindricae [S:22] superficiei. Et quoniam secans planum aut per cylindricum axem ducitur, atque ita communis sectio erit parallelogrammum; aut parallelum basibus, atque ita communis sectio circulus est; aut obliquum²⁹³ basibus²⁹⁴, atque ita communis sectio est ovalis²⁹⁵. Ideo in cylindricis tam convexis²⁹⁶ quam cavis speculis, reflexio sub triplici dispositione variabitur.