THEOREMA XXI
62 Quo minus duorum circulorum figurarumve similium similiterque positarum periferiae inter se removentur, eo magis ad unius circuli uniusve164 figurae similitudinem coeunt.
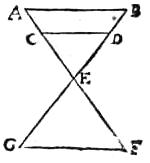
63 Ut165 si duo circuli ABCD et AECF sese in signis A, C intersecent, quo minus ipsae ABC et AEC periferiae inter se distiterint, eo magis ipsa ABCF ex periferiis utriusque circuli compacta figura ad circuli unius similitudinem accedit. Vel si duo ABC et DEF similia similiterque posita triangula sese in signis G et H intersecent, quo minus unaquaeque sese respicientia166 latera inter se distiterint, eo magis ipsa[C:13r] AGDEHBCA ex utriusque trianguli peripheriis composita figura ad unius ipsorum triangulorum similitudinem propius167 accedit.
Corollarium
64 Duorum ergo circulorum figurarumve similium similiterque positarum periferiae possunt inter se tam minime differre, ut differentia sensu nequaquam percipiatur168, ideoque uterque unus esse circulus vel utraque una esse putetur figura.