44 Theorema XVII

Radii vero intra²⁶⁵ sphaeram transparentem, a²⁶⁶ centro aeque²⁶⁷ remoti, qui paralleli non sunt, ad idem utrinque signum cum sphaerae diametro a fractionum²⁶⁸ terminis²⁶⁹ aeque distanti²⁷⁰ concurrent; sed²⁷¹ signum congressus a partibus, ad quas radii, qui²⁷² intra sphaeram, in arctum conveniunt²⁷³, propius erit²⁷⁴ ipsi sphaerae, quam reliquum.

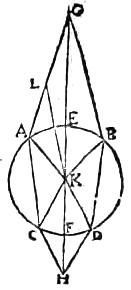
[S:41] 45 Ut si²⁷⁵ intra sphaeram abd intelligantur²⁷⁶ radii ac et bd a centro aeque remoti²⁷⁷ et ad partes c, d in arctum procedentes²⁷⁸, cum ipsa diametro ef arcus ab et cd bifariam secante, fracti ad g, h signa utrinque concurrent²⁷⁹, eritque h propinquius sphaerae quam g. Conectantur²⁸⁰ enim ipsa a, b, c, d signa cum sphaerae centro k. Eruntque, propter aequas fractiones, anguli gak et gbk invicem aequales, et²⁸¹ propter aequos arcus ae et eb²⁸², anguli quoque ake et bke invicem aequales. Sed²⁸³ ak et kb lineae²⁸⁴ aequales. 46 Ergo triangula agk et bgk sunt invicem aequilatera²⁸⁵. Et²⁸⁶ ideo ag et bg ad idem signum concurrunt. Similiter ch et dh eodem convenient. Et, quoniam propter aequas fractiones anguli gak et kch sunt aequales et latera ak et kc aequalia, ipse²⁸⁷ vero gk²⁸⁸a ipso²⁸⁹ ck²⁹⁰h angulo²⁹¹ maior²⁹² est, ideo facillime palam fit²⁹³ gk quoque ipso kh maius esse,²⁹⁴ quare²⁹⁵ et ge [C:34r] distantiam ipsa fh²⁹⁶ minorem²⁹⁷.