7
31 Si duae rectae lineae extrema singulae et media ratione secentur, totae ad maiora segmenta eandem habebunt rationem. Item totae ad minora eandem. Item segmenta segmentis proportionalia erunt.
Ut si ab in puncto c et ipsa de in puncto f extrema et media ratione secentur; quarum maiora segmenta sint bc, ef. Aio quod ab ad ipsam bc et de ad ipsam ef proportionales erunt. 32 Item ab ad ipsam ca et de ad ipsam fd proportionales. Demum bc ad ipsam ca sicut ef ad ipsam fd. Secentur enim bc, ef singulae per aequalia in punctis gh.
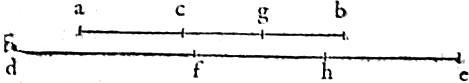
Eritque per tertiam huius, quadratum ipsius ag ad quadratum ipsius gb quintuplum. Itemque quadratum ipsius dh ad quadratum ipsius he quintuplum. Quare, per vigesimam primam Sexti, erit ag ad ipsam gb sicut dh ad ipsam he. Ergo et coniunctim, ab ad ipsam gb sicut de ad ipsam eh. Sed sicut gb ad ipsam bc sic eh ad ipsam ef. 33 Igitur ex aequali, erit sicut ab ad ipsam bc sic de ad ipsam ef et eversim sicut ab ad ipsam ac sic de ad ipsam df et disiunctim sicut bc ad ipsam ca sic ef ad ipsam fd. Quae demonstranda proponuntur. Quod si sit ab in puncto c ut supra, divisa. Et de in puncto f secta ad eandem rationem, iam facile concludetur et ipsa de in puncto f extrema similiter et media ratione secari. Unde linea in uno tantum puncto secatur extrema et media ratione.