18

71 Cubum construere, et data sphaera comprehendere, et ostendere quod ipsius sphaerae dimetiens potentia triplus est ad latus ipsius cubi.

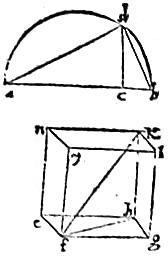
Sit datae sphaerae diametros ab ponaturque ac dupla ipsius cb sicut in pyramide. Et ipsi bd aequum sit ef latus cubi efghklmn super basim quadratam efgh erecti lateribus ad perpendiculum excitatis constructi. Ipse enim in sphaera, cuius diameter ab clauditur. 72 Cum enim ab ipsius bc tripla sit. Ideo per 8^am et 17^am Sexti quadratum ipsius ab triplum est ad quadratum ipsius bd et similiter in cubo fk diameter, connectens oppositos solidos angulos, qui demetiens est sphaerae cubum circumscribentis, potentialiter triplum ipsius ef lateris cubiti cui aequalis linea bd. Igitur fk aequalis ipsi ab propositae sphaerae diametro. Et perinde cubus ab ipsa proposita sphaera circumscribitur. Quod faciendum et demonstrandum proponitur.

fk  kh    hf  fg    gh

Igitur potentia ipsius fk ter continet potentia cubiti lateris.

73 Manifestum est igitur, quod quadrata laterum pyramidis et cubi pariter sumpta, sunt aequalia quadrato diametri sphaerae, in qua describuntur. Hoc enim quadratum uni illorum sesquialterum per antepraemissam, reliquo triplum est per praesentem. Item patet quod ac altitudo pyramidis ad bd latus vel altitudinem cubi potentialiter, est sesquitertia.