10

41 Si pentagoni aequilateri et aequianguli binos continuos angulos binae rectae subtendant, extrema et media ratione se invicem secabunt, et maiora segmenta singula erunt pentagoni lateribus aequalia.

Esto pentagonum aequilaterum et aequiangulum abcde [S:111] circulo abc inscriptum. Connexis ac be in puncto f se invicem secantibus. Aio, quod tam ac in puncto f quam be in eodem puncto secundum extremam et mediam rationem secatur et ipsa maiora segmenta cf ef singula sunt ipsis ab ae aequalia.

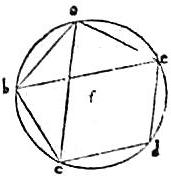
42 Nam ipsa triangula abc, bae, afb sunt similia, quoniam ad invicem aequiangula. Et quoniam angulus afe duplus est per trigesimamsecundam Primi ad angulum fba et per ultimam Sexti angulus cae duplus est ad angulum fba dictum, ideo anguli eaf et efa invicem aequales. Et illis subtensae ef, ea invicem aequales. Et similiter bc cf ostendentur aequales. 43 Quare, propter triangulorum similitudinem, sicut be ad ipsam ea et ideo ad ef sic erit ab et ideo ef ad ipsam fb idemque concludes de ipsa ca secta in puncto f. Quam ob rem tam be quam ca linea in puncto f secundum extremam mediamque rationem secatur. Constat ergo totum propositum.