[A:27r] ELEMENTORUM NONUS

p^a

1 Productus ex quadratis, sive ex similibus planis numeris¹ quadratus est.

Nam per 20^am et 19^am2 praecedentis, tam³ duobus quadratis scilicet duobus similibus planis⁴ unus interiacet medius proportionalis. Quare per ultimum corollarium 6^ae septimi, extremorum productus erit quadratus medii. 2 Contra vero, si productus ex duobus sit quadratus multiplicantes sunt similes plani. Nam inter talem quadratum et quadratum unius multiplicantium interiacet unus medius proportionalis: et unus ergo inter multiplicantes quadratis ipsis proportionales. 3 Quare per 20^am praemissi, multiplicantes plani similes sunt.

Vel quoniam per ultimum corollarium 6^ae libri 7ⁱ, radix talis quadrati sub multiplicantibus contenti est media proportionalis inter multiplicantes et ideo per 20^am praemissi, sequitur propositio. Repetatur descriptio 11^ae.

Corollarium

4 Unde patet quod si numerus quadratus multiplicans aliquem fecerit quadratum tunc multiplicatus etiam quadratus erit.

Patet ex 21^a praemissi. Quare ex quadrato in non quadratum producitur non quadratus.

2^a

5 Quadratus cubi, cubus est.

Patet in descriptione 11^ae in ordinibus obliquis et descendente ab unitate.

3^a

Cubus cubum multiplicans facit cubum

Patet in iisdem ordinibus et in transversis.

4^a

6 Item radix quadrata cubi, cubus est. Et si cubus multiplicans aliquem faciat cubum. Multiplicatus cubus est.

Constat similiter.

Corollarium

Quare ex cubo in non cubum non fit cubus.

5^a

7 Numerus primus metiens quadratum quempiam metitur etiam eius radicem.

Constat in eadem descriptione per numeros 2, 3 si ponatur uterque per se, aut alter per se primus. Idem⁵ sequitur secundum quadrato cubum, aut aliquem sequentium pones⁶ .

6^a

8 Si ab unitate disponantur numeri continue proportionales: sitque is, qui unitatem sequitur primus: eorum maximum nullus (propter praecedentes) metietur.

Patet in ordinibus obliquis, posito post unitatem primo. 9 Nam si quispiam alius numeraret quadratum 9 numerares, per praecedentem, eius radicem: quae supponitur primus numerus. Quod est impossibile. Sic etiam, si numeraret aliquem sequentium, numeraret eandem radicem astruitur ergo propositum. [A:27v]

7^a

10 Similium solidorum uterlibet ductus in alterius quadratum facit cubum.

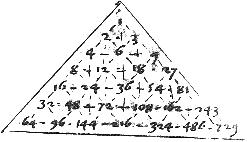
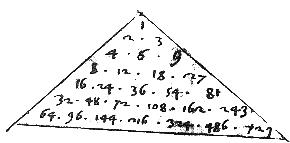
Exempli gratia, in descriptione praescripti numeri 3, 24 sunt similes solidi, quoniam habent duos medios proportionales. Eorum quadrati sunt 9 et 576. Productus autem ex 9 in 24 est 216 cubus scilicet, qui fit ex 6 in 36. Item ex 3 in 576 fit 1728 cubus videlicet qui fit ex 12 in 144.

11 Nam sicut est in descriptione 24  6 sic 36  9. Igitur per 3^um corollarium 6^ae septimi rectangulum ex 24 in 9 aequum est rectangulum ex 6 in 36 216 qui cubus est ipsius 6 quod est propositum. Item sicut est 3  12 sic 144  576 et sic 36  144. Unde per dictum corollarium rectangulum ex 3 in 576 aequatur rectangulum ex⁷ 12 in 144 1728⁸, qui cubus est ipsius 12 quod est propositum.

Similes solidi 3 9 216 cubus, qui ex 6 in 36 24 576 1728 cubus, qui ex 12 in 144

12 Quare scilicet 24  6 sicut 36  9. // Et 3  12 sicut 144  576. Vel 36  144.

Similes solidi 4 16 216 cubus, qui ex 6 in 36 13 1/2 182 1/4 729 cubus, qui ex 9 in 81

Quoniam scilicet 131/2  6 sicut 36  16. // Et 4  9 sicut 81  1821/4 vel sicut 324  729.

Scholium

Nec obstat, si per fractiones agimus cum possint redigi ad integros. Et omnis argumentatio, servata proportione procedat.

8^a

13 Similium solidorum uterlibet ductus in productum eorum facit cubum.

Exempli gratia, in superiori descriptione 3 et 24 ut dictum est, sunt similes solidi: quorum productum est 72. Itaque 3 in 72 facit 216, qui videlicet cubus est ipsius 6 in 36⁹. 14 // Quoniam scilicet 3  6 sicut 36  72, [A:28r] unde productum extremorum aequatur producto mediorum. Item 24 ductus in 72 facit 1728 cubum scilicet ex 12 in 144. Quospiam scilicet 24  12. Sicut 144  72 et perinde productum extremorum aequiperat productum mediorum.

Similes solidi 3 72 216 cubus, qui ex 6 in 36 24 1728 cubus, qui ex 12 in 144

15 Quoniam scilicet 3  6 sicut 36  72. // Et sicut 24  12 sic 144  72.

Similes solidi 4 54 216 cubus, qui ex 6 in 36 13 1/2 729 cubus, qui ex 9 in 81

Quoniam scilicet 4  6 sicut 36  54. // Et 54  9 sicut 81  131/2 vel sicut 162  27.

Scholium

Nec refert, si fractionibus utamur quoniam, cum sint magnitudines commensurabiles; redactae ad integros servant proportionem, et procedit argumentatio.

Scholium

16 Notandum etiam quod in planis similibus, et in solidis similibus, potest considerari similitudo secundum diversa latera. Ita ut laterum correlativorum proportio, in omni collatione sit eadem. Item quadrati, secundum inaequalia latera possunt esse similes plani. 17 Et cubi secundum inaequalia latera, similes solidi. Semper tamen, planorum similium ratio triplex est ad rationem respondentium laterum. Et solidorum similium ratio in triplex ad rationem correlativorum laterum.

Scholium

18 Item quicquid demonstratum est de assumptis ad exemplum numeris: transfertur ad demonstrationem aliorum quorumcumque numerorum, atque ita propositiones in totum verificantur.

9^a

19 Productus ex radicibus est radix quadrata¹⁰ producti ex quadratis. Item¹¹ est radix cubica producti ex cubis. Item radix secunda quadrata producti ex secundis quadratis. Unde¹² diviso producto radicum: per alteram radicum, divisoque producto potentiarum per potentiam dictae radicis; quotiens illius divisionis erit radix reliqua reliquae potentiae, quae quotiens est huius divisionis.

20 Iam enim patet [A:28v] in praehabita descriptione, quod positus radicibus 2, 3 earum productus est 6 qui radix quadrata est ipsius 36 quadrati, qui fit ex 4 in 9 radicum quadratis. Et radix cubica ipsius 216 cubi, qui fit ex 8 in 27 radicum cubis. 21 Demum radix secunda ipsius 1296 quadrati ipsius 36 / qui fit ex 16 in 81 radicum quadratis secundis atque idem sequitur, pro quibuscumque duobus numeris, qui pro radicibus supponantur.

10^a

22 Solidus ex ductu trium numerorum continue proportionalium genitus aequalis est cubo medii.

Capiantur in eadem descriptione 4, 6, 9 per exemplo. Iam ex horum ductu productus solidus est 216 qui cubus est ipsius 6. Item capiantur 2, 4, 8 continue proportionales. 23 Iam eorum solidus erit 64 qui cubus est ipsius 4 medii. Idem de quibuscumque numeris continue proportionalibus, in quacumque descriptione sumptis sequitur. Item hoc demonstrato in tribus numeris continue proportionalibus: transfertur demonstratio ad tres alios numeros in eadem ratione continua connexos. 24 Nam ratio respondentium laterum triplicata efficit rationem cubicam. Unde cubus illorum multiplicatus per aliquem cubum producet per 3^am huius cubum horum. Nam latera numerantur a lateribus et solidum (a solido simili per 18^am praemissi )¹³

4 6 9

216

8 12 18

1728 qui octuplus est ad 216. .

Igitur ex 8 cubo in 216 cubum per 3^am huius fit 1728 cubus

11^a

25 In superiori descriptione, si duo numeri sub unitate ponantur unitate differentes. Tunc ipsi duo numeri simul sunt differentia extremorum sequentis ordinis. Item huius ordinis trium aggregatum erit differentia extremorum tertii ordinis. Adhuc congeries quatuor numerorum tertii ordinis erit differentia extremorum quarti ordinis. Et sic deinceps in infinitum.

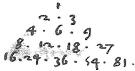
26 Hoc faciliter ostenditur, quoniam¹⁴ inferiores ordines, gignitur successive ex ductu ipsorum 2, 3 numerorm unitate di[A:29r]stantium. Atque ideo in singulis ordinibus transversis, duo quique proximi differunt per superiorem numerum. et idcirco extremi differunt per aggregatum omnium superiorum.

12^a

27 Proximi quique quadrati differunt per imparem, quem conficiunt quadratorum laterum similiter coniuncta.

Patet: quoniam in praemissa descriptione, proximi quadrati sunt 4 et 9 quoniam eorum latera sunt 2 et 3 numeri proximi. 28 Quorum quadratorum differentia, per praecedentem est ipsorum 2 et 3¹⁵ aggregatum hoc est ipse impar 5. Similter in omnibus duobus proximi quadratis quorum latera unitate distant, idem sequitur.

Corollarium

29 Hinc manifestum est, quod ex continua imparium ab unitate dispositorum additione conflantur quadrati numeri ab unitate per ordinem dispositi.

13^a

30 Proximi quique cubi differunt per aggregatum collateralium quadratorum et producti ex eorum radicibus.

Patet, quoniam proximi cubi sunt 8, 27 quorum differentia, per antepraemissam, est aggregatum ipsorum 4, 6, 9 quod sunt, extremi quadrati communes radices cum cubis sortiti: et medius 6 productus radicum 2 et 3. 31 Hoc idem de quibuslibet proximis cubis, quorum radices unitatem differunt, demonstrabimus.

Scholium

Tale autem aggregatum est numerus hexagonus aequiangulus ut in nostris Arithmeticis ostensum¹⁶ est.

Corollarium

32 Quare ex continua talium hexagonorum, post unitatem¹⁷ ordinatorum additione construuntur cubi numeri ab unitate per ordinem dispositi.

Corollarium

1 1 1   2   2 4 8 6   3 9 27   12     4 16 64       rad. cubi

1 8 7 27 19 64 37 Et deinceps.

14^a

33 Duo cubi partium cum triplis mediorum proportionalium coniuncti conficiunt cubum totius.

Exempli gratia, repetens descriptionem, dico, quod duo cubi ipsorum 2, 3 [A:29v] qui sunt 8 et 27 cum triplis ipsorum¹⁸ 12, 18 mediorum proportionalium, quae tripla sunt 36 et 54 coniuncti conficiunt cubum totius 2 et 3 hoc est cubum 125. // 34 Namque 4 in singulis 2, 3 facit singulos 8, 12.

Item duplum ipsius 6 in singulos 2, 3 facit duplum ipsius 12 et duplum ipsius 8. // Adhuc 9 in singulos 2, 3 facit ipsos 18,27 singulos. // Igitur per corollarium quintae septimi, totum 2 et 3 ductum in aggregatum ex 4 et 9 et ex duplo ipsius 6 (quod per 4^am 2ⁱ est quadratus ipsius 2, 3) hoc est, totus 2, 3 ductus in suum quadratum producet aggregatum ex ipsis 8, 27 triploque ipsius 12 ac triplo ipsius 18. 35 // Totus autem 2, 3 in suum quadratum facit suum cubum. // Ergo tale aggregatum ex 8, 27 triploque ipsorum 12, 18 est cubus totius 2, 3. Et similter in quibuscumque aliis numeris sicut in 2, 3 fecimus, ostendemus. Sicut demonstrandum proponitur.

125 25 4 2 8 aggregatum 125 3 12 12 2 24 3 36 9 2 18 3 27

15^a

36 Aggregatum proximorum quadratorum unitate superat duplum medii proportionalis

Patet, nam 4 et 9 simul excedunt duplum ipsius 6 hoc 12 in unitate quoniam differentia ipsorum 6, 9 unitate superat differentiam ipsorum 4, 6.

16^a

37 Aggregatum proximorum cuborum superat aggregatum mediorum proportionalium in aggregato radicum.

Exempli gratia aggregatum ex 8 et 27 hoc est 35 excedit aggregatum ipsorum 12, 18 quod est 30 in aggregato 2 et 3 radicum. Quoniam scilicet differentia ipsorum 18, 27 est 9 et differentia ipsorum 8, 12 est 4 quarum differentiarum excessus est aggregatum ipsorum 2, 3 per undecimam. [A:30r]

17^a

38 Ex aggregato¹⁹ radicum in productum ipsarum producitur aggregatum mediorum proportionalium inter cubos.

Exempli gratia totum 2, 3 ductum in 6 (quod est productum ipsorum 2, 3) facit aggregatum ex 12, 18. 39 // Quoniam scilicet 6 multiplicans 2, 3 singulos facit²⁰ 12, 18 singulos et idcirco per corollarium 5^ae 7ⁱ ipse 6 multiplicans 2, 3 similiter totum faciet 12 et 18 fiet²¹ quod est propositum. Et similiter in quibuslibet aliquis numeris.

18^a

40 Ex aggregato proximarum radicum in aggregatum ex producto ipsarum et unitate producitur aggregatum proximorum cuborum.

Hoc est, si ducatur totum 2, 3 in totum 1, 6 fiet aggregatum ipsorum 8, 27. // Quoniam scilicet, per praecedentem, totum²² 2, 3 in 6 facit aggregatum 1218 quod aggregatum est minus aggregato ipsorum 8, 27 in toto 2, 3 per antepraemissam. 41 Et productum ex toto 2, 3 in 6 est iam minus producto ex toto 2, 3 in 7²³ [in toto 2, 3²⁴]. Quare 6 unitate inferior est quam²⁵ 7. Et idem in quibuscumque aliis numeris concludetur.

19^a

42 Ex aggregato²⁶ radicum in aggregatum quadratorum producitur aggregatum ex cubis et ex eorum mediis proportionalibus

Hoc est ex toto 2, 3 in totum 49 fit cumulus ipsorum 8, 12, 18, 27. // Quoniam scilicet productum ex 2, 3 toto in totum 4, 9 conflatur ex quatuor productis, per corollarium quintae 7ⁱ. 43 Scilicet ex 2 in 4 et ex 3 in²⁷ 9 qui sunt duo cubi 8 et 27. Et ex 2 in 9 et ex 3 in 4 qui sunt duo medii proportionales scilicet 12, 18. // Sic constat propositum per omnibus radicibus, quamvis non unitate distantibus. Sicut 14^a et 17^a praecedentes. Nam ubi agitur de proximis quadratis, sive de proximis cubis supponuntur radices unitate distantes.

2 4 8 12 7 9 19 27

13 65 5

2 4 8 20 5 25 50 125

7 203 29

[A:30v]

44 Namque ex ductu radicum fit medius proportionalis quadratorum. Et ex ductu earundem radicum in medium fiunt medii proportionales cuborum. Et ex ductu earundem radicum directo et permutato in quadratus fiunt cubi et medii proportionales. Ut facile constat in pluries repetita descriptione.

20^a

45 Ex aggregato radicum unitate distantium in aggregatum quadratorum ipsarum radicum producitur differentia secundorum quadratorum.

Hoc est, exempli causa, ex ductu totius 2, 3 in totum 4, 9 fit 65 quae differentia est ipsorum 16 et 81 secundorum quadratorum. 46 Nam per 11^am huius, aggregatum ex 8, 12, 18, 27 est differentia ipsorum 16, 81 qui sunt quadrati ipsorum 4, 9. Et per praecedentem, ex ductu totius 2, 3 in totum 4, 9 fit aggregatum ipsorum 8, 12, 18, 27. Ergo et differentia ipsorum 16, 81 sicut hic proponitur. Et similiter per quibuscumque radicibus unitate distantibus idem sequitur.

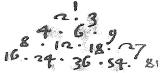
Scholium

47 Talis autem secundorum quadratorum differentia, dicitur gnomon secundorum quadratorum. Et est octahedrus centralis, cubus centralis, nec non pyramis triangula centralis, locorum imparium: ut satis ostensum est in p^o Arithmeticorum nostrorum.

21^a

48 Aggregatum ex secundis quadratis et ex quadruplo collateralium, et ex sexcuplo medii proportionalis, est secundus quadratus aggregati radicum.

Hoc est (quantacumque sit differentia ipsarum radicum) exempli gratia, in hac descriptione, dico quod aggregatum ex 16 et 81 ex quadruplo ipsorum²⁸ 4, 54 et ex sexcuplo ipsius 36 similiter consummat²⁹ secundum quadratum totius 23 quod est 625. 49 Quod [A:31r] sic demonstratur. Ex hypothesi ex 5^a septimi eiusque corollario et ex corollario 3^o sextae eiusdem libri. Iam ex toto 2, 3 in 8 fit totum 16, 24. // Item ex 2, 3 in 12 fit totum 24, 36. 50 // Adhuc ex 2, 3 in 18 fit totum 36, 54. // Item ex³⁰ 2, 3 in 27 fit totum 54, 81. // Item ex 2, 3 in triplum ipsius 12 fit totum triplum ipsius 24 cum triplo ipsius 36. // Adhuc ex 2, 3 in triplum ipsius 18 fiet totum triplum ipsius 36 cum triplo ipsius 54. // Demum ex 2, 3 in 1 fiet totum 54, 81. // Igitur per corollarium quintae 7ⁱ sequitur, ut ex 2, 3 in aggregatum ex 8 triplo quam ipsius 12 ac triplo ipsius 18 et ex 27 (quod aggregatum est cubus totius 2, 3 per 14^am huius) producatur aggregatum ex his, scilicet 16, 81 quadruplo ipsius 24 quadruplo ipsius 54 atque sexcuplo ipsius 36. 51 Sed ex toto 2, 3 in suum cubum, producitur secundus quadratus ipsius 2, 3. // Ergo talis secundus quadratus erit aggregatum ex 16, 81 ex quadruplo ipsorum 24, 54 atque sexcuplo ipsius 36. // Quod erat demonstrandum. Id idem, suppositis quibuscumque radicibus, ostendetur eodem argumenti praecessione³¹.

2, 3 8 16 24 625 12 12 12 24 24 24 36 36 36 18 18 18 36 36 36 54 54 54 27 54 81 hoc est 5 125 625 Radix in cubum ducta facit 2um tum

Scholium

52 Itaque post quatuor Elementorum geometriae libros, in quinto, per congruas diffinitiones, quidquid de ratione ac proportione praecipuum ac magis necessarium erat in sexto quidquid ad figurarum proportionem ac similitudinem spectabat. In septimo quae ad proportionem numerorum. 53 In octavo, quae ad eorum numerationem. In nono quae ad ductum faciebant, abiectis iis, quae facile notescebant [A:31v] aut quae, absque necessitate laborem accumulabantur, facilius ac brevius, item nonnulla scitu iucunda, et ab Euclide omissa, paucis hactionus³² demonstravimus. Superest negocium perfecti numeri, ut huic nono finem imponamus.

22^a

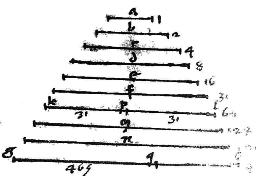
54 Si de secundo, atque ultimo numerorum continue proportionalium, aequale primo auferatur; tunc sicut erit relictum secundi ad primum, sic erit relictum ultimi ad aggregatum ex omnibus praecedentibus.

Sunto numeri quotlibet in proportione continua a, bc, d, ef quorum minimus a. 55 Et auferatur a secundo bc et ab ultimo ef ipsi cg, fh singuli ipsi a aequales. Tunc dico quod erit, sicut bg  a sic ch  aggregatum ex a, bc, d. // Ponatur enim ipsi bc aequalis fk ipsique d aequalis fl. Eruntque ef, fl, kf continue proportionales. 56 Quare, per 13^am quinti, disiunctim, erit sicut el  lf sic lk  kf et sic kh  hf. Itaque per 9^am eiusdem erit totus eh  aggregatum ex lf, fk, kf et ideo  aggregatum ex d, bc, a sicut kh  hf et ideo sicut bg  a quod est propositum. Namque bg et kh sunt aequales. Quia scilicet aequalium differentiae.

23^a

57 Si fuerint numeri ab unitate in proportione dupla continuati: quorum aggregatum sit numerus primus. Tunc ultimus eorum ductus in aggregatum producit numerum perfectum.

Sunto ab unitate a continuatim dupli numeri b,c, d, e quorum cumulus sit ipse f qui sit numerus primus. Ex e autem in f fiat gh. Tunc dico quod gh numerus perfectus est. [A:32r] 58 // Quot enim sunt ipsi b, c, d, e totidem in dupla ratione continuentur f, kl, m, n. // Eritque, sicut b  e sic f  n. Ergo quod ex b in n aequalis ei, qui ex e in f. // Sed ex e in f fit gh ergo et ex b in n fit gh et ideo gh duplus ipsius n. // Quare ipsi f, kl, m, n, gh sunt continue proportionales in ratione dupla. // Unde tam ex c in m quam ex d in kl fiet ipse gh. 59 // Quo fit, ut ipsi a, b, c, d, e singuli metiantur ipsum gh per ipsos f, kl, m, n, gh quotientes singulos. Et vicissim ut ipsi f, kl, m, n, gh singuli metiantur ipsum gh per ipsos a, b, c, d, e quotientes singulos. // Quam ob rem ipse gh habebit partes ab ipsis a, b, c, d, e et ab ipsis f, kl, m, n, gh denominatas partes autem erunt ipsi a, b, c, d, e, f, kl, m, n numeri. 60 // Auferantur ab ipsis kl, gh ipsi lp, hg singuli aequales ipsi f. // Eritque per praecedentem, sicut kp relictus  f sic gq relictus  aggregatum ex ipsis f, kl, m, n. // Verum kp aequalis ipsi f quandoquidem duplus est kl ipsius f. 61 // Ergo et gh aequalis aggregato ipsorum f, kl, m, n. // Sed hq aequalis ipso f iam aequus est et aggregato ipsorum a, b, c, d, e. // Igitur totus gh aequalis erit aggregato omnium a, b, c, d, e et ipsorum f, kl, m, n suarum partium. Nec habet gh alias partes, quam dictas. Non enim metitur ipsum gh alius numerus, quam praedicti.

62 Nam quilibet r metiatur ipsum gh secundum quotientem 5 et tunc ex r in s fit gh. Sed gh fit ex e in f. Ergo r  e sicut f  s. // Verum f primus metiens productum ex r in s iam per quintam 8ⁱ metietur alterum ipsorum r, s qui sit s. Igitur r metietur ipsum. 63 At cum b sit primus, quandoquidem binarius: atque ideo per 6^am huius, ipsum e nullus metiatur alius ab ipsis b, c, d [A:32v] propterea omnino r erit aliquis ex ipsis b, c, d atque ideo s aliquis ex ipsis k, m, n. Nam hi sint quotientes illorum: et illi horum, in dividendo ipsum gh vero si r metiatur semel³³ ipsum e. 64 Tunc s erit aequalis ipsi f. Nullus ergo numerus alius a praedictis metitur ipsum gh. // Quare gh non habet alias partes aliquotas, quam a praedictis numeris b c, a, d, e, f, kl, m, n, gh denominatas. Fuitque gh dictis partibus aequalis et idcirco per diffinitione numerus³⁴ perfectus quod erat demonstrandum.

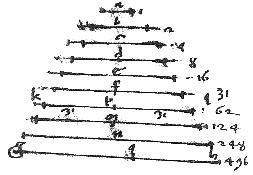
Scholium

65 Notandum est quod hic talis numerus perfectus semper est aliquis de³⁵ triangulis, et etiam aliquis de hexagonis numeris primi ordinis. sicut in primo Arithmeticorum nostrorum satis iam demonstravimus. Verum illud considera ingeniose lector, quod non solum dicta conditio facit numerum perfectum.

66 Nam et numerus impar perfectus dicitur³⁶. Par autem imperfectus. Et numerus quadratus perfectus. Parte altera longior imperfectus. Ille ex imparium: hic ex parium additione continua, conflatur. Hexagonus aequiangulus inter numerarias formas, sicut inter geometricas hexagona, est dignissimus. Quoniam hexagonorum additio continua conflat cubus. 67 Et cubi digniores quadratis. Quoniam hi quidem duplicant laterum rationem. Illi vero triplicant. Hi circulis. Illi vero sphaeris sunt proportionales. Et sphaera solidorum perfectissimum. Cuius figuram assumpsit mundus hic sensibilis, ut, quam optime posset, archetypum suum imitaretur.

22 februarii