6 19^a Tam prima⁷¹ quam secunda sectionis diametros est maxima parallelorum duaeque paralleli a centro hinc et inde aeque remotae sunt invicem aequales: contra, si paralleli fuerint aequales, erunt aeque remotae a centro.

7 Sectionis abc ipsa bd sit prima vel secunda diameter et ei parallelus a periferia ad reliquam diametrum mk⁷².

Aio quod bd est maior quam mk.

8 Namque in efg circulo, cuius semidiameter⁷³ fh perpendicularis ad eg secetur

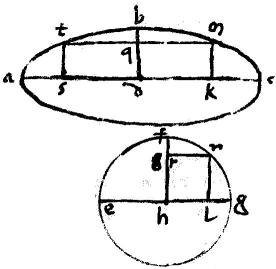
hg apud l ita ut sicut est dk ad kc sic sit hl ad lg et excitetur ad periferiam ipsi hg perpendicularis ln; eritque per alteram praemissarum, sicut bd ad mk sic fh ad nl maior autem est, per 14^am 3ⁱⁱ, fh quam nl; ergo et bd maior quam mk non aliter ostendam quod bd est maior omni perpendiculari cadente a periferia⁷⁴ abc ad diametrum ac. Itaque bd est parrallelorum maxima: quod est primum ex propositis.

Porro ponatur ipsi dk aequalis ds et excitetur ipsi ad perpendicularis st⁷⁵ ad periferiam: aio quod aequales sunt mk st.

Nam sic, erit sicut ds ad sa sic hl ad lg; quare per alteram praemissarum, erit sicut bd ad st sic fh ad nl et ideo sic bd ad mk. Ergo bd ad mk et st eandem habent rationem: quare per 9^am 5ⁱ mk st aequales, quod est altera pars propositi.

Contra, ponantur mk st aequales: aio quod et ipsae dk ds sunt aequales: nam⁷⁶ sic per 7^am 5ⁱ erit sicut bd ad mk et ideo sicut fh ad nl sic bd ad st et permutatim⁷⁷ sicut bd ad fh sic st ad nl. Ergo per 2^am partem alterius duarum praemissarum, erit sicut ds ad sa sic hl ad lg et ideo sicut dk ad kc conversim ergo et coniunctim cd ad dk sic ad ad ds aequales autem sunt dc da per diffinitionem ergo dk ds aequales, quod erat reliquum.