PROPOSITIO XXXI

241 Spatium sub spira primae et sub alia spira secundae revolutionis idem initium, eumdemque exitum habentium compraehensum, est tertia pars circuli, qui ad spiram primam primus et ad secundum secundus dicitur, et in cuius peripheria ipsae duae spirae pariter desinunt.

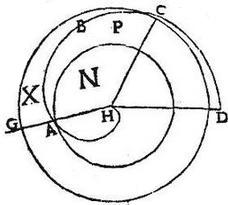
242 Sit spira primae revolutionis ABCD, et altera spira secundae revolutionis AEFGHKLD, commune initium A punctum, et commune exitum, sive terminum D punctum habentes. Quo fit, ut circulus, cuius semidiameter AD respectu quidem spirae ABCD primae revolutionis sit circulus primus; respectu vero spirae alterius AEFGHKLD secundae revolutionis sit circulus secundus, cum huius spirae pars sit spira AEFG primae revolutionis, cuius primus circulus est is, cuius semidiameter AG. 243 Erit itaque AD linea dupla ipsius AG, per 11^<am> huius, quandoquidem AD duplicem eius, quam AG peregit circularem peripheriam. [S:225] 244 Quamobrem circulus, cuius semidiameter AG erit quarta pars circuli, cuius semidiameter AD, quod et per corollarium 27^<ae> huius, patuit. Per 24^<am> autem huius, spirale spatium AFG a recta AG terminatum, est tertia pars circuli, cuius semidiameter AG, et ideo duodecima pars circuli, cuius semidiameter AD. 245 Et quoniam spiralia spatia ABCD et AEFG sunt similia, quoniam utrumque est primae revolutionis, ideo, per 29^<am> praecedentem, sunt ad invicem, sicut circuli spirarum, hoc est, sicut circulus, cuius semidiameter AD ad circulum, cuius semidiameter AG, ita spirale spatium ABCD ad spirale spatium AEFG. 246 Itaque spatium AEFG erit quarta pars spatii ABCD, spatium autem ABCD, per 24^<am> huius, tertia pars circuli, cuius semidiameter AD. Cumque spatium AEFG sit pars duodecima eiusdem circuli, erit spatium sub recta GD spirisque ABCD, AEFG compraehensum, quarta pars talis circuli. Sed, per 25^<am> huius, spatium sub spira secundae revolutionis AEFGHKLD et sub GD recta compraehensum, ad talem circulum, est sicut 7 ad 12. Igitur, quoniam de 7/12 sublata quarta parte, idest 3/12 superest pars tertia, idest 4/12. Idcirco spatium a spiris ABCD et AEFGHKLD inclusum erit pars tertia circuli, cuius semidiameter AD. Quod fuit demonstrandum.

COROLLARIUM

247 Manifestum est ergo, quod spatium sub spiris duabus, primae et secundae revolutionis idem initium, eumdemque exitum habentium interceptum, est aequale spirali spatio compraehenso sub spira primae revolutionis, rectaque extensa ad eam spiram.