F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de lineis spiralibus liber 1
<- App. -> <- = ->

PROPOSITIO PRIMA

12 Lineae a puncto aeque velociter delato peractae, sunt ad invicem sicut temporum spatia, in quibus peraguntur.

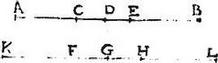
figura 1

13 Punctum quoddam aequali velocitate latum per lineam AB peragat spatia CD, DE; ipsum quidem CD in tempore FG, ipsumque DE in tempore GH. Aio iam quod sicut est linea CD ad lineam DE, sic est tempus FG ad tempus GH. Quod sic ostenditur. 14 Ponantur AD linea ipsius CD lineae, et KG tempus ipsius FG temporis aeque multiplicia. 15 Itemque BD linea ipsius DE tam multiplex, quam multiplex tempus GL [S:197] temporis GH. Sequitur ex hypothesi, ut punctum propositum peragat lineam AD in tempore KG, lineam vero BD in tempore GL. Verum si linea AD maior sit, quam linea DB, et tempus KG maius erit tempore GL, et si minor minus, et si aequalis aequale, quandoquidem supponitur punctum ipsum in maiori tempore maiorem lineam et in temporibus aequalibus aequales lineas peragere. 16 Igitur ex diffinitione proportionalis magnitudinis sicut linea CD ad lineam DE, sic erit tempus FG ad tempus GH. Quod erat demonstrandum.

Inizio della pagina
 ->