PROPOSITIO XVI

111 Si recta spiram primae revolutionis tangat, et a puncto contactus ducatur recta ad initium spirae, ducta cum tangente ad praecedentes spirae partes, obtusum facit angulum.

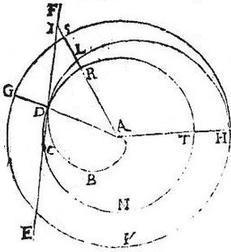
112 Esto spira ABCDH primae revolutionis, eius principium A, initium revolutionis linea AH, circulus primus HKG, linea tangens EDF, punctum contactus D. 113 Ostendendum est, quod angulus ADF obtusus est. 114 Ducatur ADG, et super centro A ad spatium AD describatur circulus DTN. Et quoniam, per 10^<am> huius, rectae a centro ad spiram continuatim crescunt, ideo circuli DTN peripheria ad partes spirae praecedentes intra spiram cadet, ad partes vero sequentes, extra. 115 Itaque, cum angulus ADF sit maior angulo portionis semicirculi, iam procul dubio non erit acutus, sed nec rectus. Esto enim, si possibile est, angulus ADF rectus. 116 Igitur, per 16^<am> tertii Elementorum, EDF contingit circulum DTN. Quamobrem, per 3^<am> huius, ab A puncto potest educi recta, quae sit ARLSI ad tangentem, secans circulum DTN apud R, tangentem apud I. Ita ut RI ad AR minorem habeat rationem, quam peripheria DR ad peripheriam DNT, igitur coniunctim ratio totius AI ad AR minor erit, quam ratio totius RDNT peripheriae¹⁴ ad DNT peripheriam, hoc est, quam SGKH peripheria ad GKH peripheriam. Sed, per 14^<am> huius, sicut SGKH peripheria ad GHK peripheriam, sic AL ad AD: ergo maior ratio AL ad AD, quam AI ad AR, et permutatim maior ratio AL ad AI, quam AD ad AR. Sed cum AD, AR [S:208] sint aequales, erit AL maior quam AI pars toto, quod est absurdum. 117 Non est igitur angulus ADF rectus, sed nec acutus fuit: superest ergo, ut sit obtusus. Id idem ostendetur, si punctum contactus fuerit in termino lineae spiralis.