PROPOSITIO III.
Conica superficies ad basim est sicut conicum latus ad semidiametrum basis.
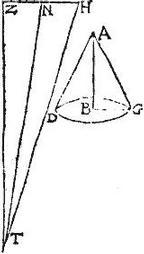
Sit conus ADG descriptus a trigono ABG angulum B rectum habente, et revoluto circa axem AB, cuius vertex A basis DG, eiusque semidiameter BG. Aio quod curva superficies coni ABG ad circulum DG est sicut hypothemisa AG ad semidiametrum BG, sit enim trigonum ZHT rectum angulum Z habens, cuius latus ZH sit aequum hypothemisae AG, ipsum vero ZT aequum periphaeriae circuli DG. Item de ZH (quae maior est ipsa BG, quoniam AG maior eadem) abscindatur ipsi BG aequalis ZN, et connectatur NT, per 4. libelli de dimensione circuli trigonum ZNT aequum circulo DG: trigonum vero ZHT per praemissam, aequum curvae superficiei coni DAG; sed per 1.6. et coniunctam proportionem, sicuti ZH ad ZN, sic trigonum ZTH ad trigonum ZTN: ergo superficies curva coni ADG ad circulum DG, sicut ZH ad ZN, et ideo sicut AG ad BG, quod erat demonstrandum. Vel sic per corollarium quartae de dimensione circuli, area circuli DG aequalis est ei, quod fit ex semidiametro BG in semiperipheriam DG. Per corollarium praemissae, conica superficies ADG aequalis est ei, quod fit ex AG latere in semiperipheriam DG: ergo adhuc per 1.6. sicut AG ad BG; sic conica superficies ADG ad circulum DG: quod est propositum.