F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis liber de sphaera et cylindro 24
<- App. -> <- = ->

PROPOSITIO XXIV.

Solidum a dimidio polygonii aequilateri circulo inscripti super diametrum stantem perfecta revolutione circumducto descriptum, aequale est ei cono, cuius basis aequalis est universae solidi superficiei, axis vero perpendiculari, quae a circuli centro ad quodlibet polygonii latus egreditur.

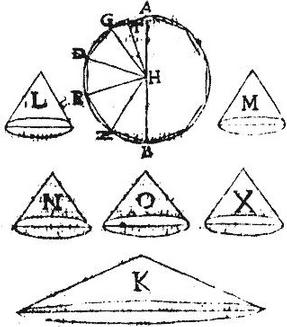
figura 31

In circulo AB, cuius diameter AB inscriptum sit polygonium aequilaterum, ut puta decagonum AB , a cuius dimidio AGDEZB super axem AB semel revoluto describatur solidum AB conicarum superficierum; ad unum autem laterum polygonii, quod sit AG, ducatur a centro sphaerae H perpendicularis HT; sitque conus K, cuius basis sit aequalis superficiei totae solidi AB, celsitudo vero aequalis perpendiculari HT. Aio quod aequalis est conus K solido AB: connectantur enim anguli G, D, E, Z, cum centro H, et constituantur coni sub celsitudine HT: videlicet conus L basim habens aequam conicae superficiei, quam describit linea AG, conus M ei, quam describit linea BZ, conus N ei, [S:70] quam describit linea GD, conus X ei, quam describit linea ZE, conus O ei, quam describit linea DE, quae cylindrica est.

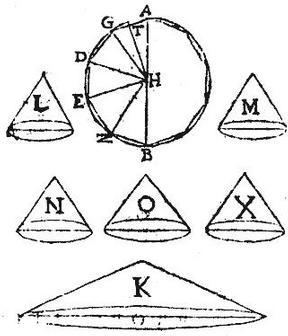
figura 32

Unde conorum L, M, N, X, O, bases simul sumptae aequales erunt universae superficiei solidi AB, et ideo aequales erunt basi coni K: quare per 21. huius, omnes hi coni L, M, N, X, O, simul aequales erunt cono K. Per primam autem partem praecedentis, solidum, quod per triangulum HAG circumductum describitur, aequum est cono L: quod autem per triangulum HBZ aequum est cono M. Item quod per triangulum HGD aequum est, per secundam partem praecedentis, cono N; quodque per triangulum HZE aequum est cono X. Quod tandem per triangulum HDE aequum est, per tertiam partem praecedentis, cono O. Itaque solidum AB, quod a toto semipolygonio ADB describitur aequum est aggregato conorum L, M, N, X, O, fuit autem hoc aggregatum cono K aequale: ergo et AB solidum cono K aequale erit: et hoc fuerat demonstrandum.

COROLLARIUM.

Manifestum est ergo quod solidum AB aequum est cylindro, cuius basis est aequalis superficiei ipsius solidi AB, axis vero aequalis tertiae parti perpendicularis HT, namque talis cylindrus per 11. et 9.12. aequalis est cono K, et ideo solido AB etc.

Inizio della pagina
 ->