PROPOSITIO XVII.
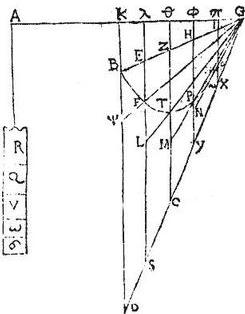
Sit rursum portio BTG contenta a recta, et sectione rectanguli coni; quae BD penes diametrum, quae GD contingens sectionem apud G; sit autem trigoni BDG tertia pars spatium Z. Aio portionem BTG aequalem esse spatio Z; nam si non est aequalis, est aut maior, aut minor: sit ergo portio BTG spatio Z maior, inquam, aliquo excessu, qui multiplicatus, sive compositus sibi ipsi poterit, per fundamentum primo assumptum, excedere trigonum BGD; multiplicetur igitur excessus, quo portio BTG superat spatium Z toties donec excedat trigonum BDG, et in totidem partes secetur BD aequales, quae sint BE, EH, HI, IK, KD, et divisionum puncta connectantur cum puncto G; connexae autem secent portionis peripheriam in punctis F, R, T, S. Itaque quoniam tota pars est trigonum BEG trigoni BDG quota pars est excessus quo portio BTG superat spatium Z suae multiplicationis excedentis trigonum BDG; ideo minus est triangulum BEG excessu, quo portio superat Z; tunc ergo portio BTG maior est quam aggregatum ex spatio Z, et ex triangulo BEG; et a fortiori trapetia BF, MR, AT, XS, et triangulum POG simul maius sunt quam spatium Z, et triangulum BEG: demantur ergo inde quidem trapetia BEF; FR, RT, TS, et triangulum GSO: hinc autem triangulum BEG predictis trapetiis, et triangulo aequale per primam sexti; et supererunt, inde quidem trapetia AF, XR, PT, et triangulum GPS, hinc autem spatium Z: maius ergo sunt trapetia AF, XR, PT, et triangulum GPS quam spatium Z: sed spatium Z per hypothesim est trianguli BCG pars tertia: ergo triangulum BDG minus est quam triplum trapetiorum AF, XR, PT, et trianguli GPS, quod per alteram praecedentium, est impossibile: non est ergo maior portio BTG spatio Z.
Sit autem nunc minor, sitque ut prius triangulum BEG minus excessu, quo spatium Z excedit portionem BTG, eritque tunc spatium Z maius quam aggregatum ex portione BTG, et ex triangulo BGE: sed trapetia BF, MR, AT, XS, et triangulum PGO per alteram praemissarum, sunt maius, quam spatium Z, quod est pars tertia trianguli BDG: igitur a fortiori trapetia BF, MR, AT, XS, et triangulum PGO maius sunt quam portio BTG, et triangulum BGE: dematur ergo utrinque portio ipsa BTG, et supererunt, inde quidem segmenta trapetiorum BF, MR, AT, XS, et triangulum PGO relicta extra peripheriam portionis, hinc autem triangulum BGE: maius ergo sunt dicta segmenta relicta extra peripheriam, quam triangulum BGE: sed triangulum BGE per primam sexti, aequum est trapetiis BF, FR, RT, TS, et triangulo SGO. Igitur dicta segmenta trapetiorum BF, FR, RT, TS, et triangulum SGO maius sunt quam ipsa trapetia, et triangulum: pars videlicet toto, quod est impossibile: non est ergo minor portio BTG spatio Z; fuitque ostensum, quod nec maior: aequalis ergo est portio BTG spatio Z, quod est tertia pars trianguli BDG: et hoc erat propositum.