PROPOSITIO III.
Parallelepipedi solidi centrum est et centrum parallelogrammi aequidistantis binis oppositis basibus, et ab utraque aequaliter remoti.
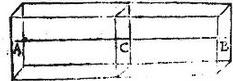
Esto parallelepipedum solidum AB, cuius bases parallelogrammae A, B quibus parallelum sit parallelogrammum C, et ab utraque aequaliter remotum, cuius centrum sit C; aio quod centrum solidi AB est ipsum C punctum: sint enim A, B, parallelogrammorum centra ipsa A, B, puncta. Eruntque A, C, B, puncta in una recta, quae axis est solidi: et quoniam per hypothesim parallelogrammum C aequaliter abest ab ipsis, A, B, parallelogrammis; ideo axis AB in puncto C per aequalia secatur: est autem AB solidum uniforme, per definitionem. Igitur per 25. primi aequalium momentorum. C punctum erit centrum ipsius parallelepipedi solidi AB; quod fuit demonstrandum.
Alia demonstratio eiusdem.
Sit parallelepipedum solidum AB, cuius bases parallelogrammae oppositae A, B, quibus parallelum medio in loco planum intersit C, cuius centrum sit C: aio quod et C centrum est solidi AB: quod sic ostenditur: sit ipsi AB solido simile, et aequale solidum DE: ita ut bases A, D sint correlativae, et bases B, E correlativae; sitque centrum solidi DE, punctum F. Et tunc si centrum C sit propinquius uni basium A, B, ut pote [S:158] basi A, quam reliquae; tunc per ultimum postulatum, et centrum F erit propinquius basi D, quam basi E: commutabo igitur collocationem basium, ita ut basis A sit correlativa basi E; et basis B correlativa basi D; (licet enim hoc propter similitudinem, et aequalitatem talium quatuor basium) atque ita fiet, ut in solidis similibus, et aequalibus AB, DE centra C, F inaequaliter removeantur a correlativis basibus A, E quod est absurdum.

Omnino igitur centrum C aeque remotum erit a basibus A, B. Similiter ostendam, quod et idem centrum C aeque removebitur a dictis duabus oppositis basibus solidi AB: nec secus, quod et aequaliter distabit a reliquis duabus oppositis basibus: sed punctum tali aequalitate ab oppositis basibus remotum est centrum parallelogrammi C. Igitur centrum solidi AB est ipsius parallelogrammi C centrum. Quod erat demonstrandum.
COROLLARIUM
Unde centrum solidi parallelepipedi semper erit illud punctum, in quo se invicem secant tres axes ipsius solidi, qui oppositarum basium centra coniungunt.
Alia demonstratio eiusdem
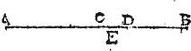
Sit parallelepipedum solidum AB, cuius axis AB, cuius medium punctum C. Aio quod centrum solidi AB est in plano parallelo basibus A, B ducto per punctum C: nam si in tali plano non sit, esto in parallelo plano per punctum D per spatium CD a puncto C medio: quare et centrum uniuscuiusque octo parallelepipedorum invicem aequalium, et similium, totalique solido AB similium recedet a medio suo per dimidium spatii CD per penultimum postulatum, quandoquidem ipsius latus dimidium est lateris solidi AB correlativum correlativi: et per consequens centrum commune dictorum octo solidorum tantumdem recedet a puncto C medio, scilicet per spatium CE dimidium ipsius CD: quapropter centrum totalis solidi AB non erit ipsum centrum commune dictorum octo solidorum; hoc est centrum totius erit aliud a centro communi omnium suarum partium: quod est absurdum. Omnino igitur centrum solidi AB erit in plano basibus A, B parallelo ducto per punctum C: similiter ostendam quod et centrum solidi AB erit in singulis planis eadem lege secantibus singulos reliquorum axium: sed hoc esse non potest, nisi centrum solidi AB sit in eo puncto, in quo tres axes solidi se vicissim secant; quod est ipsum C punctum uniuscuiusque axium medium ipsum: ergo C punctum erit solidi AB centrum. Quod fuit demonstrandum.