F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber quartus 12
<- App. -> <- = ->

PROPOSITIO XII.

In pyramide qualibet trianguli, ducto, ut praecedens, et nona huius proponit, plano; centrum facti trianguli erit centrum pyramidis.

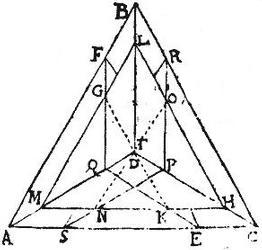
figura 20

Esto pyramis ABCD super basim triangulam ABC, ac fastigio D: secetur quaelibet hypothemisarum ut pote AD in puncto M, itaut AM sit pars tertia ipsius MD, atque per punctum M ducatur planum basi ABC aequidistans, et faciens triangulum MLH. Aio quod centrum gravitatis trianguli MLH est et centrum gravitatis ipsius ABCD pyramidis: quod sic ostenditur. Secetur rursum AD in puncto Q, itaut DQ sit pars tertia ipsius QA, sic enim DQ erit dimidium ipsius QM, et proinde ducto per punctum Q plano aequidistante ipsi basi [S:168] BCD, et faciente triangulum QFE, et secante triangulum LMH, ut sit communis sectio recta GK, erit LG dimidium ipsius GM: quare per 14. secundi momentorum aequalium, centrum trianguli LMH erit in linea GK: adhuc secetur CD in puncto P, itaut DP sit pars tertia ipsius PC, et per P punctum ducatur planum aequidistans basi ABD faciens tertium triangulum PRS; cuius item cum triangulo LMH communis sectio sit linea NO secans ipsam GK in puncto T: et ostendetur similiter LO linea dimidium esse ipsius OH: unde per memoratam 14. punctum T erit centrum trianguli LMH.

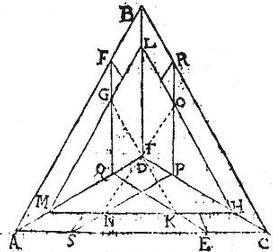
figura 21

Verum per praecedentem ter assumptam, centrum pyramidis ABCD est in unoquoque trium a ductis planis factorum triangulorum, hoc est tam in triangulo LMH, quam in triangulo QFE, quamque in triangulo PRS: omnino ergo erit in puncto tribus talibus triangulis commune: nullum autem punctum tribus ipsis triangulis est commune, nisi punctum T: igitur punctum T, quod trianguli LMH fuit, erit centrum pyramidis ABCD: quod erat demonstrandum.

Inizio della pagina
 ->