PROPOSITIO XXIX.

Si paraboles sectionis basi aequidistans linea ducatur, centrum gravitatis abscissae portionis erit propinquius vertici, quam centrum totius sectionis: linea autem inter centrum abscissae portionis et centrum segmenti aequidistantibus lineis interiecti ad lineam inter centrum dicti segmenti, et centrum totius sectionis erit sicut cubus basis ad cubum ductae aequidistantis.

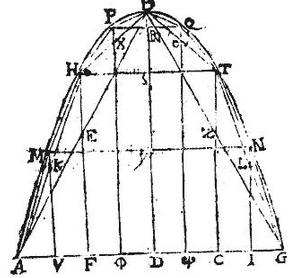
Esto parabole ABC, cuius diameter BD, basis AC, cui aequidistans sit KL, centrum sectionis ABC sit H, centrum abscissae portionis KBL, sit T; centrum segmenti AKLC, sit E: et cum per 6. primi momentorum aequalium, centrum totius sit inter centra partium; erit iam centrum H, inter centra T, E, et perinde centrum T abscissae partis propinquius erit vertici, quam H centrum. Quod est primum ex propositis. Item dico, quod linea TE ad lineam EH, erit sicut cubus, qui ex AD ad cubum qui ex KS. Nam per 27. primi momentorum aequalium; gravia reciproca sunt spatiis, quibus eorum centra distant a centro communi: atque ideo erit, sicut linea TH ad lineam HE, sic iam segmentum AKLC ad portionem abscissam KBL: et coniunctim sicut linea TE ad HE, sic tota ABC sectio ad portionem abscissam KBL: sed per 26. huius, sectio ABC ad portionem abscissam KBL est sicut cubus, qui ex AD ad cubum, qui ex KS: igitur erit utique sicut cubus qui ex AD ad cubum, qui ex KS: sic linea TE ad lineam EH: quod erat demonstrandum.