F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber tertius 27
<- App. -> <- = ->

PROPOSITIO XXVII.

figura 28

Si intra conicam sectionem, quae parabole dicitur, figura rectilinea perspecte inscribatur, abscissae portiones a coniungentibus angulos a vertice per ordinem ad verticem receptae erunt ad invicem in proportione cuborum numerorum ab unitate ordinatorum.

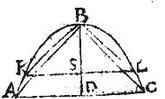
Repetatur descriptio 15. huius: in qua demonstrandum est, quod portiones PBQ, HBT, MBN, ABG sunt in proportione cuborum numerorum ab unitate: namque per 15. huius, ipsae lineae PR, HS, MY, AD sunt in proportione numerorum ab unitate per ordinem natura[S:154]lem procedentium: et per praecedentem, praedictae portiones sunt in proportione cuborum, qui ex ipsis PR, HS, MY, AD fiunt: cubi autem tales sunt, qui ab unitate per ordinem disponuntur: igitur portiones PBQ, HBT; MBN, ABG sunt in proportione cuborum numerorum ab unitate ordinatorum: quod erat demonstrandum.

Inizio della pagina
 ->