PROPOSITIO XIX.
Centrum gravitatis sectionis conicae, quae vocatur parabola, est in diametro sectionis.
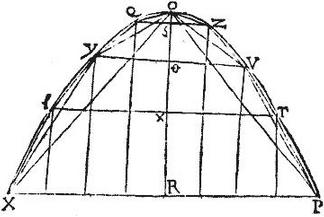
Esto parabola ABC, cuius basis AC, diameter BD: aio quod centrum gravitatis paraboles ABC, erit in diametro BD, sit enim centrum, si possibile est, extra diametrum, in puncto E: sitque EF ipsi BD aequidistans, et inscribatur sectioni triangulum ABC habens eandem axem, et basim; et sicut est CF ad FD, sic sit triangulum ABC ad quadrilaterum K: et inscribatur parabolae figura perspecte ita ut relictae portiones sint minus, quam quadrilaterum K; eritque per 17. huius, inscriptae figurae centrum in diametro BD: sit itaque centrum ipsum punctum H, tum coniungatur HE, et producatur; et CL aequidistet ipsis BD, EF, quibus peractis maior erit ratio figurae inscriptae ad relictas portiones, quam trianguli ABC ad quadrilaterum K, hoc est, quam CF ad FD, hoc est, quam LE ad EH: sit ergo sicut figura inscripta ad relictas portiones, sic ME ad EH; et quoniam E centrum est totius scilicet paraboles: centrum autem unius partis, scilicet figurae inscriptae est H punctum. Ideo per 35. primi aequalium momentorum, erit punctum M centrum reliquae partis integrantis totum, hoc est portionum relictarum. Verum si M punctum est centrum ipsarum relictarum portionum, sic centrum gravitatis est extra ambitum gravis: quod per ultimum postulatum, est inconveniens: superest ergo ut centrum sectionis ABC omnino sit in diametro BD. Sicut proponitur demonstrandum.