F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber tertius 1
<- App. -> <- = ->

Propositiones, quarum multa sunt theoremata, non nulla vero problemata.

PROPOSITIO PRIMA.

Si latera trapetii, aequidistantia singula bifariam secentur, puncta sectionum, et punctum coincidentiae reliquorum laterum erunt in eadem recta linea.

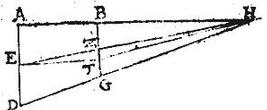
figura 1

Esto trapetium ABGD, cuius latera AD, BG aequidistantia singula per aequalia secentur in punctis E, Z reliqua vero latera AB, DG coincidant in puncto H: aio iam quod puncta E, Z, H sunt in eadem recta linea, hoc est quod recta linea EH incedit per punctum Z, coniugatur enim EH, et incedat, si possibile est, per aliud, quam Z punctum, ut per T punctum; eritque propter triangulorum similitudinem BT ad AE, sicut HT ad HE, et sicut HT ad HE, sic TG ad ED: igitur sicut TG ad ED, sic BT ad AE; et permutatim sicut BT ad TG, sic AE ad ED: aequalis autem per hypothesim AE ipsi ED: ergo et BT aequalis ipsi TG: fuit vero per hypothesim BZ aequalis ipsi ZG igitur BZ, BT dimidiae sunt eiusdem BG, et proinde aequales: pars et totum, quod est absurdum: omnino itaque recta EH it per punctum Z: quapropter puncta E, Z, H sunt in eadem recta: quod erat demonstrandum.

Inizio della pagina
 ->