PROPOSITIO XIV.

Rectilineorum, quae ex trapetiis numeri eiusdem, sive ex trapetiis numeri eiusdem, et ex triangulis singulis ad verticem, qualibus dictum est, componuntur, (si aequidistantia latera respondentia ipsorum fuerint proportionalia, et axes respondentium trapetiorum proportionales): centra gravitatum similiter dividunt axes.

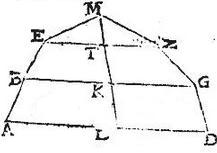
Sunto duo rectilinea ABG, DEZ, quorum ipsum ABG componitur ex trapetiis duobus HK, KL, et ex triangulo LB: ipsum autem DEZ ex duobus trapetiis TM, MN, et triangulo NE, itaut sicut est latus AG ad latus DZ, sic caetera latera aequidistantia in rectilineo ABG ad caetera latera aequidistantia in rectilineo DEZ, singula singulis correlativis conferendo, existant: item, sicut est axis HK ad axem TM, sic KL ad MN, atque sic LB ad NE, totales autem axes BH, ET per aequalia secent unumquodque aequidistantium laterum in trapetiis; horum itaque duorum rectilineorum ABG, DEZ centra gravitatum, per praemissam 13. vel ante praemissam 12. erunt in axibus BH, ET: sint ergo centra puncta O, V, in axibus. Demonstrandum est, quod talia puncta similiter, hoc est ad eandem rationem secant axes, ut scilicet si[S:143]cut est BO ad OH, sic omnino sit EV ad VT; id enim sequitur, quoniam centra partialium trapetiorum proportionaliter dividunt partiales axes per 11. huius, et centra triangulorum proportionaliter secant axes per 24. praecedentis libelli, sint enim centra triangulorum P, Q centra trapetiorum LK, MN puncta R, S: centra trapetiorum KH, MT puncta Y, F. Eruntque portiones axis BH proportionales partibus axis ET: nam per 24. praecedentis, in triangulis ipsa BP dupla ipsius PL, et EQ dupla ipsius QN, et per 11. huius, in trapetiis, sicut est LR ad RK, sic NS, ad SM, et sicut KY ad YH, sic MF ad FT, quo fit ut segmenta axis BH segmentis axis ET sint proportionalia, singula singulis; quandoquidem axes partiales trapetiorum, et trianguli axibus partialibus trapetiorum, et trianguli proportionales supponuntur: ut igitur BP ad EQ sic PL ad QN, sic LR ad NS, sic RK ad SM, sic KY ad MF, sic YH ad FT. Et quoniam proportionalia supponuntur, latera aequidistantia trapetiorum, et proportionales axes: ideo sicut trapetium HK ad trapetium KL, sic iam trapetium TM ad trapetium MN. Trapetiorum itaque HK, KL centrum commune sit X; trapetiorum vero TM, MN centrum commune sit C, et quoniam per 27. praemissi, gravia reciproca sunt distantiis, quibus eorum centra absunt a communi centro, ideo erunt sicut quadrilaterum HK ad quadrilaterum KL, sic linea RX ad lineam XY, et similiter sicut quadrilaterum TM ad quadrilaterum MN, sic linea SC ad lineam CF, sed eadem fuit ratio trapetiorum: igitur sicut linea RX ad XY, sic linea SC ad lineam CF.

Unde sequitur ut puncta X, C cadant inter correlativa puncta, utque ad eandem rationem dividant axes BH, ET: quoniam igitur trapetiorum HK, KL tamquam unius centrum est X, et trianguli LB tamquam unius centrum P, sit centrum amborum commune O, eritque ut prius, sicut aggregatum ex trapetiis HK, KL ad triangulum LB, sic linea PO ad lineam OX, et similiter sicut aggregatum ex trapetiis TM, MN ad triangulum NE, sic linea QV ad lineam VC: quandoquidem V est centrum commune duorum gravium, hoc est trapetiorum TM, MN tanquam unius, et trianguli NE tanquam alterius, hoc est totius rectilinei DEZ. Sed sicut aggregatum trapetiorum HK, KL ad triangulum LB, sic trapetia TM, MN simul ad triangulum NE, quandoquidem proportionalia supponuntur latera aequidistantia, et axes. Igitur sicut linea PO ad lineam OX, sic linea QV ad lineam VC; unde sequitur ut puncta O, V cadant inter correlativa puncta, utque ad eandem rationem dividant axes BH, ET. Quamobrem ex tali divisione proportionali, erit sicut BO, ad OH, sic EV ad VE, quod iam proponitur demonstrandum.

Quod autem trapetium HK ad trapetium KL sit sicut trapetium TM ad trapetium MN: patet quoniam eorum latera aequidistantia supponuntur proportionalia, et axes item proportionales, ex quorum ratione componuntur arearum rationes: namque trapetii area producitur ex axe in dimidium aggregati ex aequidistantibus lateribus. Quando axes perpendiculares sunt lateribus.

Similiter illud idem ostendemus de rectilineis, quae ex quotcumque trapetiis tantum, vel ex quotcumque trapetiis, et singularibus triangulis, sub dicta conditione componuntur; nam tali aequidistantium laterum, et ex axium proportione supposita sequi[S:144]tur similis axium divisio, ut scilicet proportionales sint inter axium segmenta, inter correlativa centra iterum, atque iterum recepta: sicut proponebatur demonstrandum.

Quando autem axes non sunt perpendiculares lateribus, tunc pro axibus sumantur perpendiculares inter latera aequidistantia, tales enim perpendiculares sunt proportionales axibus aeque inclinatis; et trapetii area producitur tunc ex perpendiculari inter aequidistantia latera in dimidium aggregati ex ipsis aequidistantibus.