PROPOSITIO VI.
Centrum totius est in recta coniungente centra partium.
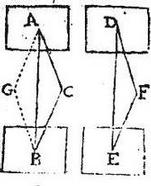
Totum grave sit AB, partes eius A et B, centra gravitatum partium A, B, sint puncta A, B; coniungatur AB: aio itaque quod centrum totius AB est in ipsa recta linea AB; collocetur enim grave AB itaut linea AB sit perpendicularis ad horizontem; et in tali situ suspendatur pondus A; pendebit namque per 3. huius, itaut locatum est. Suspendatur item grave B ab ipsomet puncto A, pendebit enim per 3. sic similiter, ut locatum est: et totum igitur AB ita pendebit a puncto A, ut fuit locatum; fuit autem AB posita perpendicularis ad horizontem: igitur per 2. huius, centrum gravis AB suspendi a puncto A in ipsa est AB linea: quod erat demonstrandum.
Aliter sic. Sit, si possibile est, centrum gravis AB extra AB lineam in puncto C: et coniungantur AC BC, et exponantur duo gravia D, E ipsis A, B singula singulis aequalia, et in eodem intervallo DE: et ipsi ABC triangulo aequilaterum triangulum sit DEF, atque triangulum ABG: ita enim coaptatis triangulis ABC, DEF, congruet grave A gravi D, atque grave B gravi E, propter aequalitatem, et similitudinem (quae supponenda est) et centrum gravitatis C congruet puncto F. Quare quoniam congruentium gravium congruunt gravitatum centra; estque gravis AB centrum C, erit iam et gravis DE centrum F. congruat vero rursum triangulum DEF triangulo ABG. Rursus enim et gravia D, E gravibus A, B commutatis lateribus, propter uniformitatem (quae supponitur) congruent: tunc ergo centrum gravitatis F [S:90] puncto G congruet, non autem ipsi centro gravitatis C: congruentium ergo gravium AB, DE non congruunt centra C, F: quod est absurdum per sextum postulatum.