PROPOSITIO XXXXVII.
Si centrum aggregati ex quatuor gravibus sit in sectione linearum, quae centra binorum oppositorum coniungunt; illud idem erit centrum commune tam his duobus oppositis, quam illis.
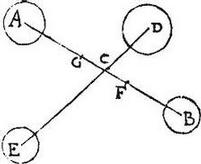
Sint quatuor gravia A, B, E, D, et lineae AB, ED coniungentes oppositorum centra. Secent se invicem in puncto C, sitque punctum C centrum aggregati ex gravibus A, B, E, D: dico quod ipsum erit centrum commune ipsorum AB, itemque C erit centrum commune ipsorum DE: nam si C non sit centrum commune ipsorum A, B sit ergo F, erit quippe in linea AB per 6. huius; quare FC producta ibit per centrum commune ipsorum D, E per 7. quod sit G. Itaque centrum ipsorum D, E non erit in linea DE iungente centra, quod per 6. est impossibile: igitur non erit aliud, quam C punctum commune centrum ipsorum A, B: et per eandem ostendetur non esse aliud quam idem C punctum commune centrum ipsorum D, E: quod erat demonstrandum.