PROPOSITIO XXXXII.

Eisdem suppositis demonstrandum est, quod sicut est excessus segmentorum ad segmentum minus, sic erit adiectum ad totum grave uniforme.

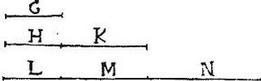
Hoc est, sicut est excessus segmenti maioris CA (in praecedenti figura) super segmentum minus BC collatum ad ipsum segmentum minus BC, sic est ipsum F adiectum ad totum grave AB: nam cum gravia BC, CA atque aggregatum ex BC et F sint continue proportionalia; sint (facilioris intelligentiae causa) huiusmodi trium gravium primum G, alterum HK, tertium LMN, sic videlicet disposita, ut G, H, L sint inter se aequalia; item K, M inter se aequalia, ut scilicet K vel M sit excessus ipsius HK super G: ipsum autem N excessus ipsius LMN super HK, et ideo totum MN excessus eiusdem LMN super G; sic enim fit ut G, sit ipsum BC segmentum minus HK ipsum CA segmentum maius; K eorum excessus: LMN aggregatum ex BC et F; atque MN ipsum adiectum F: cum L sit ipsi G, et perinde ipsi BC aequale: itaque demonstrandum est quod sicut est K ad G, sic iam erit MN ad totum G, HK: hoc modo; cum HK ad G sit sicut ipsum LMN ad HK, erit disiunctim K ad G sicut N ad HK: quare per 13.5. elementorum, erit, et sicut K ad G, sic aggregatum ex K, N, hoc est MN ad aggregatum ex G, HK, et hoc iam fuerat demonstrandum.

COROLLARIUM.

Unde manifestum est, quod si segmentum maius sit duplum minoris, tunc adiectum est aequale toti gravi uniformi: si triplum, tunc adiectum fit duplum totius: si quadruplum; tunc adiectum fit triplum totius, et sic deinceps: item si segmentum maius sit sesquialterum minoris, tunc adiectum fit dimidium totius: si sesquitertium: tunc adiectum fit tertia pars totius: si sesquiquartum, tunc adiectum fiet quarta pars totius, itaque deinceps.