F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber primus 40
<- App. -> <- = ->

PROPOSITIO XXXX.

Si uniforme grave suspendatur a puncto, ad quod copulantur axes partium inaequalium: ratio factorum momentorum erit, quae partium ipsarum duplicata.

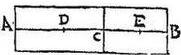
figura 37

Sit uniforme grave AB circum axem AB, quod secetur in duo segmenta inaequalia, quorum axes AC, CB ad punctum C continuati, et suspendatur grave AB a puncto C: aio quod ratio momenti AC ad momentum CB erit sicut ratio gravis AC ad grave CB duplicata: secetur enim per medium axis AC in puncto D, et axis CB in puncto E: eruntque per 25. huius, ipsa D, E puncta centra gravium AC, CB: itaque per 3. huius, ipsa AC, CB gravia pendebunt a punctis D, E suspensa, et perinde ad spatia DC, [S:105] CE: quamobrem per praecedentem; ratio momenti AC ad momentum CB, componetur ex ratione gravis AC ad grave CB, et ex ratione spatii DC ad spatium CE: sed per 26. huius, sicut axis AC ad axem CB, et ideo sicut DC spatium ad CE spatium, quae sunt axium dimidia, sic grave AC ad grave CB: igitur ratio momenti AC ad momentum CB componetur ex duabus rationibus, quarum utraque est ratio gravis AC ad grave CB: itaque ratio momenti AC ad momentum CB est sicut ratio gravis AC ad grave CB duplicata: quod fuit demonstrandum.

COROLLARIUM.

Unde si pars ad partem sit dupla momentum ad momentum erit quadruplum: si pars ad partem tripla: momentum ad momentum erit nonuplum.

Inizio della pagina
 ->