PROPOSITIO XXVII.

Si circulus, et ellipsis, sive duae ellipses positae sint inter lineas aequidistantes: erunt ad invicem sicut earum diametri, quae lineis dictis aequidistant.

Sit circulus, sive ellipsis ABCD, cuius centrum E, item ellipsis FGHK, cuius centrum L: positae inter lineas aequidistantes BG, DK, quae tangant ellipses in ipsis B, G, D, K, punctis; quo fit ut lineae BD, GK, quae tactuum puncta coniungunt eant per sectionum centra E, L, ex 6. et 27. secundi conicorum Apollonii utque AEC, FLH tangentibus aequidistantes sint [S:270] per 47. et 15. primi conicorum ordinate ad diametros BD, GK; et perinde secundae diametri. Et earum paralleli ordinate ad easdem diametros BD, GK. Itaque demonstrandum est, quod sectio ABCD ad sectionem FGHK est sicut diameter AC ad diametrum FH; sit enim sicut linea AC ad lineam FH, sic sectio ABCD ad circulum M. Itaque ostendendum est, quod circulus M aequalis erit sectioni FGHK; secus enim sit circulus M maior ellipsi FGHK; et inscribatur circulo M multiangula figura maior ellipsi FGHK, et totidem laterum figura inscribatur tam sectioni ABCD, quam sectioni FGHK, ductis aequidistantibus, quae secent diametros BD, GK, sicut aequidistantes ab angulo ad angulum secant diametrum circuli M: eritque figura ABCD ad figuram FGHK sicut linea AC ad lineam FH. Quoniam scilicet trapetia finiuntur basibus superis, et inferis proportionalibus; per 25. primi conicorum et ideo sunt lineis correlativis proportionales: unde trapetia adiuncta ad trapetia, hoc est figura ad figuram est sicut linea ad sibi correlativam lineam.

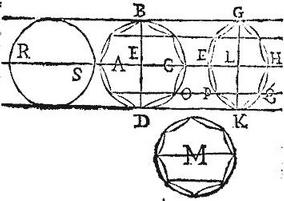
Igitur sicut figura ABCD ad figuram FGHK, sic erit sectio ABCD ad circulum M; sed sectio ABCD ad circulum M, est sicut figura ABCD ad figuram M; (hoc enim sequitur, supposito primum, quod sectio ABCD sit circulus.) Ergo sicut figura ABCD ad figuram M, sic figura ABCD ad figuram FGHK. Aequalis est ergo figura FGHK figurae M: quare figura M minor erit ellipsi FGHK; fuerat vero maior, quod est absurdum. Non est igitur circulus M maior ellipsi FGHK. Sit deinde minor; et tunc inscribatur ellipsi FGHK multiangula figura FGHK maior circulo M; et inter easdem aequidistantes figura totidem laterum inscribatur sectioni ABC (quae primum circulus supponatur esse) et ei similis inscribatur circulo M: eritque rursus figura ABCD ad figuram FGHK, sicut linea AC ad lineam FH, sed sic dudum fuerat sectio ABCD ad circulum M: atque sic est figura ABCD ad figuram M. Igitur figura ABCD ad figuram M, sicut figura ABCD ad figuram FGHK: aequalis ergo est figura FGHK figurae M. Quare circulus M maior quam ellipsis FGH; fuerat autem minor; quod est absurdum: non est itaque circulus minor ellipsi FGHK; sed nec maior fuit. Aequalis ergo erit: quod fuit demonstrandum.

Supponatur nunc ellipsim esse ABCD, et id idem demonstrabitur. Ponatur enim inter easdem aequidistantes circulus RS: et eodem modo demonstrabimus, quod ellipsis ABCD ad circulum RS erit sicut linea AC ad diametrum RS, quodque circulus RS ad ellipsim FGHK erit sicut diameter RS ad lineam FH: unde ex aequali ordinata concludemus, ellipsim ABCD ad ellipsim FGHK esse sicut linea AC ad lineam FH. Quod est propositum. [S:271]

SCHOLIUM.

Iisdem autem suppositis ostendemus, quod portiones circuli, et ellipsis, sive duarum ellipsium a linea tangentibus aequidistante abscissae, sunt proportionales.

Nam si de circulo ABCD capiamus portionem NDO; de ellipsi autem FGHK capiamus portionem PKQ per lineam NQ, ipsis BG, DK aequidistantem abscissas: tum de circulo M portionem similem portioni NDO: iam per figuras in assumptis portionibus inscriptas, eodemque syllogismo adversarium confutantes, demonstrabimus, quod portio NDO ad portionem PKQ est sicut diameter AC ad diametrum FH, vel sicut quaelibet chordarum ad quamlibet correlativarum chordarum: atque ideo per 19. quinti Euclidis sic esse portionem NBO relictam ad portionem PGQ relictam: sic esse totam ABCD ad totam FGHK sectionem.

COROLLARIUM.

Ex quibus manifestum est, quod si circulorum, sive duarum ellipsium tangentibus lineis interpositarum secundae diametri fuerint aequales, circuli ipsi, sive ipsae ellipses aequales erunt: et earum portiones per lineam tangentibus aequidistantem abscissae ad invicem aequales erunt; et bases portionum aequales.