PROPOSITIO XXIII.

Sphaera, et sphaeroides, sive duae sphaeroides figurae communem axem habentes, sunt quadratis reliquarum diametrorum proportionales.

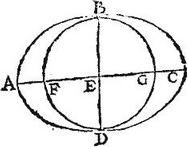
Sit circulus ABCD, sive ellipsis, cuius centrum E; sit item circa eumdem axim; centrumque alia ellipsis DFBG: ac manente immoto axi BD circuli quidem revolutione sphaera; ellipsium vero circumlatione sphaeroides figurae describantur: sintque secundae diametri ad rectos axi ipsae AC, FG. Dico itaque, quod sphaera, sive sphaeroides ABC, ad sphaeroidem figuram FBG est sicut quadratum AC ad ipsum FG quadratum. Nam per demonstrata de sphaera, et cylindro, atque per praecedentem, sphaera, sive sphaeroides ABC dupla est ad conum, cuius axis BD, basisque circulus AC, rectus axi BD; sphaeroides quoque FBG duplum est ad conum, cuius axis BD, basisque circulus FG axi rectus. Igitur sphaera ABC, sive sphaeroides ad sphaeroidem FBG est sicut conus, cuius basis AC ad conum, cuius basis FG, quorum altitudo communis BD: sed conus ille ad hunc per 14. premissi, est sicut basis ad basim; et ideo sicut quadratum AC ad ipsum quadratum FG (quandoquidem circuli sunt quadratis diametrorum proportionales.) Igitur et sicut quadratum AC ad quadratum FG, sic sphaera sive sphaeroides ABC ad sphaeroidem figuram FBG. Quod erat demonstrandum.