F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de conoidibus et sphaeroidibus figuris Liber secundus 12
<- App. -> <- = ->

PROPOSITIO XII.

Si ab extremo diametri maioris, ellipsis in conoide solido parabolico factae, perpendicularis ducatur ad lineam, quae per centrum ellipsis axi solidi aequidistans incedit; ducta perpendicularis aequalis erit semidiametro minori ellipsis praedictae.

Esto solidum conoides a parabola ABC, cuius axis BG descriptum; in quo quidem ducto plano ad axem obliquo per 23. praemissi, sectio fiat ellipsis, cuius diameter AE, in quo centrum ellipsis sit punctum F: ductaque DF ad aequidistantiam axis BG, productaque excipiat perpendicularem AK. Demonstrandum est, quod AK est aequalis semidiametro minori ellipsis AE. Ducatur enim per punctum F pla[S:256]num rectum super axem BG faciens per 17. praemissi, in solido circulum, cuius diameter CGFH, et cuius cum ellipsi communis sectio sit linea FP; itaque tam circuli CH, quam ellipsis AE peripheria incedet per punctum P: eritque FP minor semidiameter ellipsis APE per 23. praecedentis.

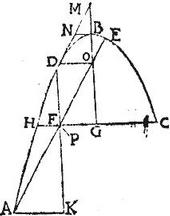
figura 9

Demonstrandum est itaque quod AK aequalis est ipsi PF; hoc modo. Ducatur per punctum D ipsi AE aequidistans DM occurrens axi GB producto apud M: nam cum DF sit diameter ipsius AE ordinatae, ordinata erit DM, et ideo per 32. primi conicorum elementorum tangens erit sectionem apud D; occurrat ipsi tangenti DM, ipsa BN ad rectos axi: quae similiter parabolam tanget apud B; eique aequidistans sit DO. Unde per 35. primi conicorum MB aequalis erit ipsi BO, et ideo MN aequalis ND: cum autem BN, ND tangentes aequidistent ipsis CFH, AFE se vicissim apud F secantes iam per 17. tertii conicorum erit sicut quadratum DN ad quadratum NB, sic quadratum AF ad rectangulum CFH, hoc est sicut quadratum MN ad quadratum NB, sic quadratum AF ad quadratum PF. Cum ergo proportionalia sint quadrata linearum; et ipsae lineae proportionales erunt: hoc est sicut MN ad NB, sic AF ad PF; simile autem est triangulum FAK, triangulo MNB (quandoquidem eorum latera singula unius singulis alterius aequidistant:) itaque proportionalia sunt eorum latera respondentia: quare sicut MN ad NB, sic FA ad AK. Eamdem igitur habet rationem linea AF ad lineam FP, et ad lineam AK: aequalis ergo est linea AK ipsi PF. Et hoc erat demonstrandum.

SCHOLIUM.

Notandum, quod haec propositio addita fuit ad demonstrationem sequentis.

Inizio della pagina
 ->