PROPOSITIO XIII.
Quod si excitata sit super diametrum minorem perpendicularis nihilominus idem possibile fore ostendetur.
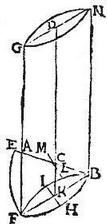
Rursum sit ellipsis cuius diameter maior AB, minor CEF, sese in E centro secantes; excitata autem ED, perpendicularis sit ad CEF, non autem ad AB. Aio rursum quod cylindrus aliquis est habens axem ED, atque suscipiens in superficie cylindrica ellipsim AB; producatur enim ED, et per puncta A, B, C, F ipsi ED aequidistantes, donec, compleantur duo rectangula AGM, LKN seinvicem in rectum secantia; existente communi sectione linea DEH erecta super AG, LK; et circa diametros AG, KL si aequales sunt circulus describatur AKG, si inaequales ellipsis AKG; si enim circulus sit AKG, tunc cylindrus habens pro basibus circulum AKG, eique aequalem, et aequidistantem super centro D descriptum, et axem DH suscipit in superficie cylindrica ellipsim AB propositam: quandoquidem extrema diametrorum AB, CF talis ellipseos sunt in cylindrica superficie. Si vero AKG non circulus sit, sed ellipsis tunc cum HD excitata perpendicularis sit super diametrum maiorem ellipsis AKG. Iam per praemissam, cylindrus aliquis erit habens axim HD, atque suscipiens in superficie cylindrica ellipsim AKG; et is igitur idem cylindrus suscipiet ellipsim propositam AB; quoniam videlicet et in eadem cylindrica superficie continuantur lineae per puncta A, B, C, F ductae, et axi aequidistantes: et perinde in eadem superficie constituuntur extrema diametrorum propositae ellipsis.
SCHOLIUM.
Notandum quod praemissae quatuor propositiones, quae ab Archymede obscurissimo, ac difficili processu traduntur, hic multo apertius demonstrantur; atque id auxilio conicorum, ac cylindricorum elementorum, quae ab Apollonio, et Sereno post Archimedem, copiosius tradita sunt.