(corso di LaTeX in
 puntate)
puntate)
 puntate)
puntate)Riccardo Murri
<murri@phc.unipi.it>
``TeX è progettato in modo da permettere di scrivere facilmente espressioni matematiche complesse. L'idea alla base è che una formula complicata è composta di formule meno complicate combinate in maniera semplice; le formule meno complicate sono, a loro volta, fatte di combinazioni semplici di formule ancora meno complicate; e così via. [...] Partiamo allora da quelle semplici e apriamoci una strada verso l'alto.'' -- da: Donald E. Knuth, ``The TeX book'', 1986
Questo paragrafo di Knuth spiega praticamente tutto quello che c'è da sapere per capire come TeX costruisce le formule: TeX legge il testo che corrisponde ad una formula e ne divide i contenuti in formule più semplici, e prosegue fino a scomporre queste in formule elementari; costruite queste, le combina a seconda del modo in cui sono legate insieme (per esempio numeratore e denominatore di una frazione), poi combina le espressioni così ricavate e via via risale fino a comporre la formula originaria.
Vediamo cosa succede in pratica. Le formule più semplici sono
costituite da una singola lettera oppure un singolo numero; per
inserirle in un documento LaTeX dovremo scrivere, ad esempio,
\(x\) o \(2\). Se scriviamo \(2 x\) allora TeX
scomporrà questa formula nei due costituenti elementari, e poi
accosterà il prodotto di questi due. Se invece scriviamo
\(x = 2\) allora questa volta LaTeX inserirà un leggero
spazio tra ``x'' e ``='', come anche tra ``='' e ``2'': TeX
riconosce che il segno ``='' lega le due formule semplici ai
suoi lati in maniera diversa da uno spazio.
Schematicamente, ecco le differenze principali fra il modo matematico (math mode) e quello di testo.
\par
fermeranno TeX con un errore. Vedremo più avanti come fare per
mostrare più formule o equazioni di seguito.
Fin qui la teoria; distingueremo allora i comandi TeX per comporre formule in base a come legano insieme le varie espressioni.
Per prima cosa, ogni documento LaTeX che utilizzi notazioni matematiche dovrebbe caricare le estensioni amsmath con il comando
\usepackage{amsmath}
nel preambolo. Tutti gli esempi nel seguito usano questa estensione.
Ogni formula matematica deve essere racchiusa tra i comandi
\( e \). Il primo di questi comandi pone TeX in
modo matematico, ed il secondo ne esce. Le formule matematiche
seguono regole di composizione tipografica differenti dal testo
ordinario; perciò è necessario racchiudere le formule tra i due
particolari indicatori \( e \) (math brackets, o
parentesi matematiche): in questo modo TeX userà le convenzioni
tipografiche e di input proprie delle formule.
Il modo più semplice per combinare delle espressioni è tramite i
simboli di operazioni e relazioni: alcuni sono già presenti sulla
tastiera (+, -, =, ecc.) per gli altri LaTeX
ha una serie di comandi specifici. TeX tratta tutti questi comandi
come se fossero un nome lungo per un solo carattere: ad esempio, il
comando \cup produce il simbolo di unione di insiemi,
LaTeX lo tratta allo stesso modo del segno +. Ricordate di
mettere sempre uno spazio alla fine di questi comandi: si scrive
\alpha X e non \alphaX altrimenti TeX cercherà di
chiamare il comando dal nome alphaX, che non è definito.
Una formula si può allora scrivere mettendo insieme, come se scrivessimo un'espressione con carta e penna:
+, -, *, /,
...);
<, >, =, ...);
!, :, ;, ...);
{ e } hanno un significato speciale per TeX, quindi
occorre precederle con una barra inversa \ per produrre il
corrispondente segno.
Figure 1:
Esempi di formule molto semplici.

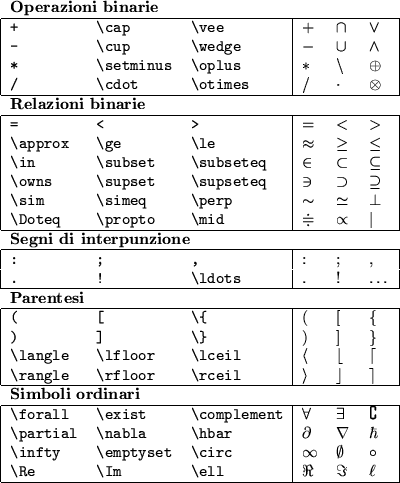
Un catalogo dei simboli più comuni è in figura 2; una lista completa si può trovare alle pagine 19-21 della ``Users' guide to AMSFonts'', che troverete nel file amsfndoc.dvi sotto la directory /usr/doc/texmf/fonts/amsfonts/. Chi usa AUC-TEX può attivare il menu matematico premendo Control-c ~ e poi scegliere il simboli che gli servono dalle voci del menu. Per accedere a tutti questi simboli è necessario caricare l'estensione amsfonts, aggiungendo il comando
\usepackage{amsfonts}
al preambolo di un documento.
Figure:
Alcuni dei simboli che si possono inserire con
LaTeX in una formula matematica. Una lista molto più completa si
trova in ``Users' guide to AMSFonts'', pp. 19-21
Per inserire dello spazio in una formula si usano i comandi
\quad e \qquad; il secondo produce uno spazio maggiore
del primo.
Per inserire qualche parola di testo ordinario, si può usare il
comando \text. Questo comando accetta un solo argomento, il
testo da inserire. Tutti i comandi che abbiamo visto la volta scorsa
per manipolare il carattere del testo vanno bene per inserire del
testo in una formula matematica, ma non sono adatti per comporre
sottoformule.
Provate a vedere cosa viene fuori da:
\(f(x)=0 \quad \text{se e solo se} \quad g(x)=0\)
E se leviamo i comandi \quad? Se togliamo \text e
lasciamo ``se e solo se'' in mezzo?
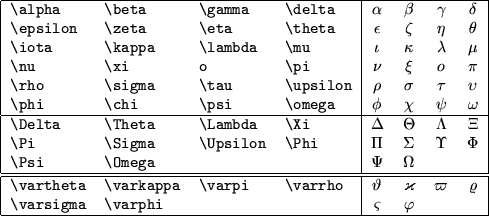
Figure:
I comandi TeX per produrre le lettere greche, minuscole e
maiuscole. La lettera omicron è identica alla ``o'' latina,
come pure molte le maiuscole che non compaiono nell'elenco: non
c'è quindi bisogno di comandi particolari. L'ultima riga contiene
i comandi per produrre alcune varianti grafiche.
Il comando \frac serve a combinare due espressioni matematiche
in una frazione. Questo comando accetta due argomenti: il primo è il
numeratore, il secondo il denominatore. Qualunque espressione
matematica può andare al numeratore o al denominatore: guardate gli
esempi di figura 4.
\cfrac è una variante di \frac adatta alla composizione
di frazioni continue. Cosa succede se usate \lcfrac o
\rcfrac al suo posto?
Figure 4:
Esempi di frazioni e coefficienti binomiali.
![\begin{figure}
\begin{center}
\begin{tabular}{\vert l\vert r\vert}
\hline
\e...
...c <134>>1{{1+\dotsb}}$\ \\ [1ex]
\hline
\end{tabular} \end{center}\end{figure}% WIDTH=618 HEIGHT=192](img5.png)
Il comando \binom combina due espressioni a formare un
coefficiente binomiale; accetta due argomenti, nello stesso ordine di
\frac.
\sqrt pone un segno di radice quadrata sopra l'espressione
matematica che ne costituisce l'argomento. È possibile specificare un
argomento opzionale, che indica l'ordine della radice:
\sqrt[3]{x} è la radice cubica, ecc. Alcuni esempi si trovano
in figura 5. Cosa succede se si mette un'espressione
matematica più complicata (per esempio \frac{p}{q}) come
radicando? E come ordine della radice?
![\begin{figure}
\begin{center}
\begin{tabular}{\vert l\vert r\vert}
\hline
\e...
...} + \sqrt[\beta]{x-t}$\ \\ [1ex]
\hline
\end{tabular} \end{center}\end{figure}% WIDTH=477 HEIGHT=130](img6.png)
Si può aggiungere un esponente a fianco di qualunque simbolo col
comando \sp o un indice con \sb. Come per quasi tutti i
comandi, se l'argomento di \sp o \sb consta di più di un
carattere, occorre racchiuderlo entro le parentesi { e
}. Al posto di \sp e \sb si possono usare
i caratteri ``^'' e ``_''. Esempi di espressioni con
esponenti e deponenti sono in figura 6.
Figure 6:
Espressioni con esponenti e deponenti. Negli ultimi due
esempi si usa la formula nulla {} per forzare la
posizione di indici che altrimenti verrebbero spostati a sinistra.

Qualunque espressione matematica può comparire come esponente o indice
di un'altra, purché racchiusa tra { e }. In
particolare, gli esponenti possono a loro volta contenere altri
esponenti, deponenti, ecc. (cfr. figura 6) Cosa succede a
mettere una frazione come esponente? Provate con
H^{p+\frac{n}{m}}. E se si usano le varianti \dfrac e
\tfrac?
Un simbolo può avere anche simultaneamente esponenti e
deponenti, e non conta l'ordine con cui sono indicati. Ancora,
l'espressione nulla {} può a sua volta avere esponenti o
deponenti, e questo permette di metterne alla sinistra di un
simbolo: {}_2F_3 produce le due espressioni F_3 e
{}_2, che vengono poi accostate, cosicché l'effetto finale è
quello di un deponente ``2'' alla sinistra della ``F''. Cosa succede
se, dimenticando {}, uno scrive X + _2F_3?
Attenzione! TeX considera un errore scrivere due esponenti
o due deponenti di seguito: x^y^z e x_y_z sono
sintatticamente ambigui; occorre perciò usare le parentesi graffe per
raggruppare correttamente i termini: x_{yz} o x_{y_z}, a
seconda di ciò che si intende. Il carattere ' (apostrofo)
è considerato un esponente in modo matematico: perciò non si
deve scrivere F'^2 ma {F'}^2 (Quiz: perché F^{'2}
non va bene?).
I caratteri ``^'' e ``_'' vengono usati in TeX anche
per indicare gli estremi di integrazione: nella figura 7
introduciamo le prime formule con integrali e sommatorie, che altro
non sono, per il TeX, che nuovi simboli, un po' più grandi.
Oltre ai simboli mostrati in figura 7, LaTeX definisce
anche \iint, \iiint, \iiint e \idotsint
per gli integrali doppi, tripli, quadrupli e multipli; troviamo anche
le versioni \big degli operatori binari come \vee,
\wedge, \otimes, ecc. : abbiamo così \bigvee,
\bigwedge, ecc.
Tutti questi simboli accettano ``limiti'' che possono essere inseriti come se fossero esponenti e deponenti; non è necessario che i limiti siano presenti: è permesso specificarne uno solo, entrambi o nessuno.
Figure:
Formule con integrali, sommatorie ed altri
operatori. Tutti questi costituiscono una classe di simboli che
ha lo stesso comportamento in TeX: hanno due dimensioni
possibili, e usano la notazione degli indici per fissare i
``limiti''. Il posizionamento degli indici cambia se la formula
è nel mezzo di un brano di testo (inline math) o a sé
stante (display math).
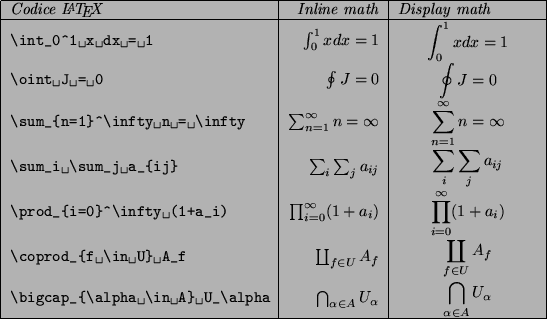
L'intestazione della figura 7 distingue due colonne,
chiamate inline math e display math, cui corrispondono
dimensioni diverse per i simboli matematici nella tabella. Il modo
matematico di TeX ha infatti due varianti: la prima serve per
comporre formule che vengono inserite in una riga di testo, la seconda
per formule che appariranno a sé stanti, interrompendo il normale
flusso della parola scritta; la figura 8 riporta un
esempio di entrambe. Le formule inline sono racchiuse
dai comandi \( e \), quelle displayed sono
circondate dai comandi \[ e \].
Figure 8:
Un esempio della differenza tra formule inline e displayed.
![\begin{tabular}{\vert p{0.5\textwidth}\vert p{0.5\textwidth}\vert}
\hline
\beg...
... \sum_{i=0}^n a_i$.\end{verbatim} \end{minipage} \\ [1ex]
\hline
\end{tabular}% WIDTH=595 HEIGHT=127](img9.png)
Le funzioni matematiche più comuni vengono di solito rese in carattere
dritto per farle risaltare all'interno di una formula e
distinguerle dalle variabili, che sono in corsivo. Perciò LaTeX definisce i comandi \log, \sin, \cos,
ecc. La figura 9 riporta un elenco completo.
Figure 9:
Funzioni e operatori comuni predefiniti in LaTeX.

È anche possibile definire nuove funzioni, tramite il comando
\DeclareMathOperator; questo comando vuole due argomenti, il
primo dei quali è un comando da definire (completo di \) ed il
secondo il testo che apparirà come nome della funzione. Per esempio,
se volessimo chiamare ``sen'' la funzione seno, potremmo dare a
LaTeX il comando
\DeclareMathOperator{\sen}{sen}
e poi scrivere formule come \(y = \sen x\).
Alcuni dei comandi riportati in figura 9 non corrispondono in realtà a delle funzioni matematiche, ma a degli ``operatori'', intendendo con questo che TeX permette di specificare degli estremi come per i simboli di integrale, sommatoria, ecc. La figura 10 riporta alcuni esempi: la differenza con un simbolo di funzione si vede solo in modalità display math.
È possibile definire anche nuovi operatori, tramite il comando
\DeclareMathOperator*: la sintassi è identica a quella di
\DeclareMathOperator, l'unica differenza sta nella possibilità
di specificare gli estremi con la notazione degli esponenti.
Figure:
Esempi di simboli di operatori: il posizionamento dei
deponenti è analogo a quello dei simboli di integrale,
sommatoria, ecc.
![\begin{tabular}{\vert l\vert p{0.25\textwidth}\vert}
\hline
\verb*'\lim_{x\rig...
...\le i \le N}
a_i\end{displaymath}\end{minipage} \\ [1ex]
\hline
\end{tabular}% WIDTH=437 HEIGHT=98](img11.png)
Se avete provato a scrivere qualche formula in TeX, mentre leggevate questo articolo, non vi sarà sfuggito che le parentesi (e con questo intendo i delimitatori nel gergo di TeX) non si allargano automaticamente a coprire le formule che racchiudono: il dimensionamento corretto delle parentesi intorno ad una formula è un compito complesso, quindi occorre istruire appositamente LaTeX.
I comandi \left e \right tentano il dimensionamento
automatico delle parentesi, calcolando la minima altezza necessaria a
racchiudere tutta l'espressione che circondano. Ciascuno di questi
comandi deve essere seguito da un delimitatore valido: una parentesi
oppure uno dei simboli della figura 2. \left e
\right devono sempre essere appaiati, ma i loro argomenti no:
si può, ad esempio, aprire un'espressione con una parentesi tonda e
chiuderla con una quadra. In particolare, se l'argomento di uno dei
due è il carattere ``.'', allora il corrispondende delimitatore
è invisibile: questo si può usare come nel terzo esempio di
figura 11.
Figure 11:
Esempi di dimensionamento delle parentesi.
![\begin{tabular}{\vert l\vert p{0.25\textwidth}\vert}
\hline
\verb*'\left[ x^y ...
...}{b'} \Bigr\rvert\end{displaymath}\end{minipage} \\ [2ex]
\hline
\end{tabular}% WIDTH=496 HEIGHT=146](img12.png)
left e \right è adeguato nella maggior parte
dei casi, ma ci sono tre situazioni in cui è opportuno dimensionare
manualmente le parentesi:
\left e \right
contiene esponenti o deponenti: in questi casi la dimensione
calcolata automaticamente risulta essere maggiore di quella
necessaria;
\left e
\right e fanno tutte le parentesi della stessa dimensione
(perché tanto basta per racchiudere un'espressione);
Si può ricorrere al dimensionamento manuale con i comandi riportati in
figura 8; la sintassi è la stessa di \left e
\right.
Figure 12:
Le varie dimensioni disponibili per il dimensionamento manuale delle parentesi.
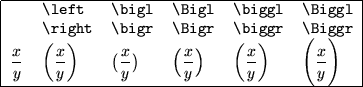
La lunga tirata è finita: riposiamoci...
 puntate)
puntate)This document was generated using the LaTeX2HTML translator Version 98.2 beta6 (August 14th, 1998)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -white -address Riccardo Murri
The translation was initiated by Riccardo Murri on 1999-10-21