Reverendi Do. Francisci
Maurolyci, abbatis messanensis,
atque mathematici celeberrimi.
DE SPHAERA LIBER UNUS
Ad lectorem prologus
1 De sphaera, et de computo temporum multos olim scripsisse constat: inter quos Io. Sacroboscus, Robertus Episcopus Lingoniensis, et Campanus praecipui sunt. Lubet tamen hic paucis perstringere quidquid pertinet ad huiusmodi negocium. Sphaerae quidem tractatus continet astronomica rudimenta: computus autem kalendarii, festorum mensium: et anni rationem, quasi quaedam ad calculum introductio. 2 Quare, sicut sphaera videtur esse theorica quaedam motuum, ita computus praxis eorundem et supputatio. Et utrunque usu venit publicae commoditati. Utrinque enim derivatur, fastorum, temporum, lunationum, ac solemnitatum distinctio, et annorum ordo, secundum Consules, Caesares, Pontifices, Reges, et historias succedentium; [S:2] atque quotidianus rationum et negocium usus. 3 Tentabimus igitur et nos horum principia et praecepta subtexere. Fortasse aliquid ab aliis omissum, supplebimus: aut, si opus fuerit superflua resecabimus. Utroque enim modo hallucinantur authores. Et brevior traditio facilius percipitur. Quis nescit Campanum, tam in sphaera, quam in computo tam diffuse locutum non ad negocii necessitatem, sed ad ostentationem: utque Sacroboscum inscitiae pariter argueret? 4 Sed utinam ipse in traditione Elementorum Euclidis, suo nimium confisus acumini non errasset, et Io. Regimontii limam non sensisset. Sed haec alibi discutientur.
De scientiarum divisione.
Quoniam omnis scientia versatur circa subiectum, de quo tractat: est in subiecto, hoc est in anima: dicitur de subiecto, ut generalis de particulari. 5 Propterea philosophia distingui potest per tres modos. Primo, secundum divisionem subiecti, ut in organicam er realem, sicut subiectum in signum et rem significatam. Secundo, secundum obiecta potentiarum animae: ut in consyderationem veri, quod est obiectum intellectus; et boni, quod est obiectum voluntatis. Tertio, secundum divisionem generis in species: ut in Theoricam et Practicam, quae sunt duae praecipuae species Philosophiae.
6 Praeterea Scientia praecedit Scientiam quinque modis. Primo, ut generalis particularem. Exempli gratia, Philosophia universas, Mathematica Geometriam, Logica Grammaticam. Secundo, propter ordinem inventionis, sicut cognitio particularium praecedit cognitionem universalium: ubi a sensu procedimus ad intellectum. 7 Tertio, in processu discendi, seu docendi: sicut Grammatica praecedit Rhetoricam, et Dialectica caeteras. Quarto, nobilitate subiecti: sicut Theologia praecedit Astronomiam, et Astronomia Geographiam. Quinto, certitudine demonstrationis, ut Geometria praecedit Astronomiam, et Astronomia Physicam.
[S:3] Secundum divisionem subiecti.
Philosophia
Organica vel Logica
|
||||||||||||||||
Realis
|
Secundum obiecta potentiarum.
Philosophia circa obiectum intellectis vel voluntatis
Verum circa speculationem
|
|||||||||||||||||||||||||||
Bonum circa praxim
|
Secundum divisionem generis in species.
Philosophia
Theorica
|
||||||||||||||||||
Practica
|
Sic per triplicem respectum, Philosophia tribus modis distingui potest. Nec te lector ingeniose moveat diversitas positionum: quandoquidem in unaquaque trium divisionum Scientiae, et artes (utcunque disponantur) semper invicem cognatae, et ab eadem radice propagatae consistunt.
Quoniam itaque Speculativa pars Philosophiae dividitur in natu[S:4]ralem, Mathematicam, ac Theologiam. Atque Theologia excedit facultatem humanam. Physica vero, propter materiae fluxum, incerta. Idcirco commendatur Mathematica, et praecipue Astronomia, propter certitudinem demonstrationis, et subiecti nobilitatem, ut ait Ptolemaeus. Igitur Astronomiae principia tradituri, praemittemus quaedam geometrica, et necessaria praeambula.
Geometrica principia.
Punctum est signum quantitatis expers. Linea est longitudo latitudine carens. Linearum quoque alia recta, alia flexa. Superficies est, quae longitudinem et latitudinem habet. Superficierum alia plana, alia curva. Angulus est linearum concursus indirectus. Angulorum alius rectilineus, alius alterius modi. Recta in rectam perpendicularis est, cum utrinque angulos facit aequales, qui recti dicuntur. Angulus recto maior, obtusus: minor autem acutus dicitur. Terminus est limes, seu finis. Figura est, quae termino, vel terminis clauditur. Circulus est figura, cuius centrum a periferia aequaliter distat: hunc diameter per centrum ducta in semicirculos dividit: recta vero praeter centrum in portiones inaequales. Rectilinearum figurarum quaedam sunt trilaterae, quaedam quadrilaterae, quaedam multilaterae. Triangulorum autem quoddam aequilaterum: quoddam isosceles, quod duo tantum latera aequalia habet: quoddam scalenum, quod tria inaequalia. Item aliud orthogonium, quod unum ex angulis rectum: aliud amblygonium, quod unum obtusum: aliud oxygonium, quod omnes acutos habet. Semper autem maius latus opponitur angulo maiori. Et anguli tres coniuncti conficiunt duos rectos. Quadrilaterarum figurarum quinque sunt species, quadratum, rhombus, rectangulum, rhomboides, et trapezium. Ex quibus prima et secunda sunt aequilaterae solum prima et tertia rectos habent angulos. Secunda et quarta oppositos angulos habent aequales. Tertia et quarta latera etiam opposita aequalia. Postrema vero neque aequilatera, neque aequiangula est. Rectae autem paralleli, sive aequidistantes sunt, quae in eodem plano descriptae quorsumcunque et quantumcumque protractae contactum non admittunt. Parallelogrammum est, cuius opposita latera aequidistant. Quales sunt aequilaterarum primae quatuor species. Limites et coincidentiae linearum sunt puncta. Cuiuslibet figurae rectilineae anguli omnes coniuncti conficiunt tot paria rectorum, in quot triangula dividuntur. Unde quatuor anguli figurae quadrilaterae conflant quatuor rectos, quia resolvitur in duo triangula. Anguli figurae pentagonae conflant sex rectos, quoniam secatur in tria triangula, et sic deinceps. [S:5]
Solidum est corpus sub triplici dimensione contentum hoc est, quod longum, latum et profundum est. Perpendicularis recta in planum est, quae rectos facit angulos cum rectis in plano ductis. Parallela plana sunt, quae quoquo versum et quantumcunque producta nusquam coincidunt. Parallelepipeda solida sunt, quorum oppositae bases sunt parallelae. Solidorum species sunt pyramides, columnae, prismata, atque polyedrae figurae. Angulus solidus fit ex concursu trium, vel plurium angulorum planorum, quos necesse est quatuor rectis angulis esse minores. Ex polyedris figuris solidis quinque tantum sunt, quae regularia dicuntur, quoniam sub aequilateris, et aequiangulis et aequalibus inter se basibus singula continentur. Pyramis, scilicet quatuor triangulis. Octaedrum octo. Cubus sex quadratis. Icosaedrum triangulis viginti. Dodecaedrum duodecim pentagonis. Conus est pyramis rotunda super basim circularem. Cylindrus columna rotunda, pro basibus habens circulos aequos et parallelos. In his axis per verticem et centra basium ducitur. Qui cum perpendicularis est, est ad basim, conus et cylindrus dicetur rectus. Secus autem scatenus. Tam duae rectae se invicem secantes, quam omne triangulum rectilineum in uno iacent plano. Sphaera est solidum sub una superficie conclusum, a qua centrum medium aequaliter distat. Eius diameter vel axis per centrum incedit, ut Theodosium. Vel solidum, quod a semicirculo super fixam diametrum circunducto describitur. ut ait Euclides. Ratio seu proportio est quantitatum eiusdem generis collatio. Similes, eaedem, vel aequales rationes sunt, quae vel eiusdem sunt nominis, vel qualibet nominata ratione simul sunt maiores, vel simul minores. Nominatur autem ratio a numeris. Eiusdem rationis quantitates proportionales dicuntur.
Similes planae, similiterque positae figurae sunt, quarum anguli singuli singulis aequales et totidem. Et latera singula singulis proportionalia, et aequidistantia. Similia et similiter collocata solida sunt, quae sub similibus et eiusdem numeri basibus, et parallelis continentur. Et fieri potest interdum, ut in positione simili planarum duo latera figurarum, vel bina congruant simul. Et in locatione simili solidarum, duae bases, vel binae, vel ternae communicent uni plano, reliquis aequidistantibus. Correlativa latera, vel correlativas bases, correlativis singulas singulis conferendo. Item similes coni, aut similes cylindri sunt quorum axes sunt basium diametris proportionales, et recti vel aequaliter inclinati. Omnes autem duo circuli, et omnes duae sphaerae sunt ad invicem similes, quoniam semper habent diametros perimetris proportionales. Item in circulis chordae proportionales diametris abscindunt similes portiones, quae suscipiunt aequos angulos, sive ad cen[S:6]trum, sive ad periferiam positos. In sphaeris quoque circuli (quorum diametri sphaericis diametris proportionales) similes abscindunt sphaericas portiones. Tam autem parallelogrammum ad suum triangulum, quam columna tetragona ad suum serratile, dupla est. Item tam columna ad suam pyramidem, quam cylindrus ad suum conum triplus est. Item duo triangula, duo parallelogramma, duae columnae, duae pyramides, sive coni super aequas bases constituti sunt fastigiis proportionales: si autem sunt eiusdem altitudinis, sunt basibus proportionales. Item anguli in circulis, sive ad centrum, sive ad periferiam terminat, sunt assumptis periferiis proportionales.
Similes autem planae figurae sunt in dupla ratione respondentium laterum. Sic et duo circuli in dupla ratione diametrorum. Similia vero solida sunt in tripla ratione correlativorum laterum. Sic et duae sphaerae, in ratione diametrorum triplicata. In caeteris autem figuris, sive in planis triangula, sive parallelogramma conferas, sive in solidis pyramides, aut parallelepipeda, vel columnas conferas. Semper collatarum figurarum ratio, ex rationibus basium et celsitudinum componetur. Unde, si bases fuerint celsitudinibus reciprocae, figuras aequales esse necesse est. Et e contrario.
Quando autem recta secat duas parallelos, tunc tam anguli contrapositi, quam coalterni, quam extrinsecus et intrinsecus oppositi sunt invicem aequales. Et duo intrinseci simul duobus rectis angulis aequales. Et una ex his conditio facit aequidistantiam. Quando linea secat lineam, duo anguli collaterales aut sunt recti, aut duobus rectis aequales. Et omnes quatuor anguli, aut recti, aut quatuor rectis simul aequales. Unde quatuor quadrata simul, vel tria hexagona aequiangula, vel sex triangula aequilatera implere possunt totum spacium, concurrentibus angulis. Quoniam scilicet angulo in quadrato rectus est. In hexagono valet unum rectum et tertiam partem. In triangulo valet duas tertias unius recti. Et idcirco tam quatuor angulos quadrati, quam tres angulos hexagoni, et quam tres angulos trianguli, quatuor rectis angulis aequivalere necesse est. Item, si quantitatem angulorum pensitas, sicut hexagonos cum intermistis triangulis, ita octagonos cum intermistis quadratis compaginatos totum locum implere tam ratione, quam experientia concludes. Haec autem ex Euclidis Elementis praelibanda sunt et praediscenda his, qui astronomica principia capessere volunt. Sed et sphaericas Theodosii elementa minime omittenda sunt, ut Sphaerae mundanae forma, circulorum magnitudo, situs, inclinationes, axes, et poli, et divisio intelligantur.
Si planum secet sphaeram per centrum, sectio erit circulus maior habens commune centrum cum sphaera, eamque secans in duo hemi[S:7]sphaeria. Si autem planum secet sphaeram praeter centrum, sectio erit circulus minor, centrum habens extra sphaerae centrum, et sphaeram secans in duas inaequales portiones. Unde circuli maiores omnes in sphaera sunt invicem aequales, et se invicem in semicirculos dividunt: quoniam commune centrum habent. Circuli autem minores aequaliter remoti a centro sphaerae sunt aequales. Remotior autem minor. Axis sphaerae est eius diameter super quo movetur. Et est eius circuli, per cuius centrum perpendiculariter transit. Poli sunt axis extrema, quae singula aequaliter removentur a sui circuli periferia. Circuli paralleli in sphaera habent eundem axem, et eosdem polos, et e contrario. Circulus maior in sphaera incedens per polos circulorum aequidistantur: dividit eos singulos per aequalia. Si autem praeter polos, per inaequalia (excepto maiori aequidistantur) arcus autem coalterni duorum circulorum utrinque aequaliter a medio remotorum, sunt aequales. Et remotior, maiorem patitur inaequalitatem. Idemque facit maior obliquitas secantes. Circulus maior ductus per polos circulorum in sphaera se invicem secantium, dividit utrasque portiones eorum per aequalia, se vero contingentium, transit per punctum contactus. Si duo circuli maiores eant per polos circulorum aequidistantium, vel tangant eorum minimum. Tunc horum arcus inter semicirculos maiorum recepti sunt similes: et maiorum arcus aequidistantibus duobus inclusi sunt aequales.
His praemissis, veniemus ad sphaerae mundanae introductionem. Quidquid autem super isto negocio tradendum est, aut pertinet ad principia, aut ad circulos, aut ad motum primum, aut ad motus secundarios. Haec singula summatim ac paucis explicabimus.
Sphaerae principia, quae sunt sex Ptolemaei conclusiones.
Coeli figuram esse sphaericam, et motum eius circularem. Nam coelo universa comprehensuro congrua fuit forma capacissima ad motum circularem facilis, et quae semper intra eosdem se limites contineret: et talis est sphaerica. Item si secus esset, coeli propter plures motus circulares frangerentur, aut vacuum in eis reperiretur. Id idem sensibili comprobatur experimento. Quod autem astrorum corpora sunt sphaerica, constat: quoniam quaqua versum spectata rotunda videntur. Item a necessitate motus ab exemplo coelestis et elementariis formae. A cremento et decremento Lunae.
Terram esse rotundam. Nam rotunditatem ab ortu ad occasum arguit anticipatio ortuum et occasuum stellarum per indicium [S:8] lunaris eclipsis. Rotunditatem ab austro ad boream indicant crementa meridianarum altitudinum et polorum mundi. Quod autem talis rotunditas sit circularis, patet, quoniam anticipationes dictae, atque crementa sunt spaciis locorum proportionalia. Quod aqua sit rotunda, ostenditur a dictis argumentis. Item ab apparitione successiva scopulorum, arcium, insularum. Quod globus totus sit rotundus similiter ostenditur. Item ab umbra terrae in deliquo Lunae. Ab aequali nisu in centrum, et ab aequali distantia a centro. Quod totus mundus sit rotundus, comprobatur a similitudine mundi archetypi. Terra tamen ob duritiem non potuit perfectam rotunditatem adipisci: sed montium eminentiae, aut valles ad tantam molem collatae non sentiuntur.
Terram in medio mundi sitam esse. Id enim sequitur, cum de toto coelo hemisphaerium, de circulis magnis semicirculos videamus, neque aliter constarent crementa dierum, ac noctium, neque lunares eclipses, neque umbrarum aequinoctialium termini in rectam lineam desinerent. Item cum demonstratum sit eam in duabus mundi diametris esse, sequitur ut sit in centro. Idem poscit lex naturae gravia in medium compellentis.
Terram respectu firmamenti quasi punctum esse ostenditur haec similiter. Secus enim non videremus dimidium coeli, et dimidia magnorum circulorum. Et distantia centrorum instrumenti et terrae inferret sensibilem in observationibus diversitatem. Item stella in motu primo non appareret eiusdem semper magnitudinis. Adhuc cum minima stellarum (quae maior est, quam terra) sit respectu firmamenti quasi punctum, argumentum sumetur a fortiori.
Quod terra localem motum non habet, ostendere. Nam per motum rectum relinqueret centrum, et minus gravia restarent in medio. Per motum vero circularem super alium axem ab axe mundi, variaretur altitudo poli. Super axem vero mundi, relinqueret, quaecunque sunt in aere versus occidentem aedificia corruerent. Et lapis sursum iactus non eodem recideret. Essetque contra naturam stabilitatis terrae.
Motus coelestes in duplici differentia reperiri nam motus primus, per quem Sol et astra omnia oriuntur et occidunt, et revolutionem in spacio diei naturalis perficiunt, super axe polisque Mundi, omnibus est cognitus. Secundarius vero huic contrarius ab occasu ad ortum Solis, Lunae ac planetarum super axe Zodiaci, patet ex quotidiana observatione, et ex varia ipsorum velocitate. Unde notescit ex numero motuum et velocitate numerus, et ordo sphaerarum coelestium, scilicet primi mobilis, coeli stellati Saturni, Iovis, Martis, Solis, Veneris, Mercurii, atque Lunae: sicut postea distinctius explicabimus. Haec sunt principia Astronomiae, quae praedictis et aliis argumentis demon[S:9]strantur. Non enim sunt per se nota, sicut arithmetica et geometrica, et pure mathematica fundamenta.
De Mundo.
Mundus est sphaera, cuius centrum est ipsum universi, terraeque centrum: superficies vero ipsa primi mobilis, sive coeli ultimi convexa. Cum autem sphaera sit solidum, solidum autem superficie, vel superficiebus claudatur, superficies vero linea vel lineis terminetur, linea denique punctis interiaceat; idcirco Astronomiam capessentibus istaec fundamina sunt praeiacienda, imo non solum Geometria, sed Arithmetica etiam praecepta praelibanda.
De Axe, polisque.
Axis autem mundi diameter est huius sphaericae machinae, super quem sphaera ipsa vel Mundus vertitur ab ortu ad occasum poli vero sunt axis puncta extrema. Unde omnia astra, omnes stellae, imo omnia, quaecunque in mundo sunt, puncta motu circulari feruntur, et circulos describunt eo maiores, quo ab axe, polisque remotiores poli autem, et quaecunque in axe sunt puncta stabilia manent, et axis totus fixus, et perpetuo semper motui sufficiens.
De Aequatore.
Nunc autem de sphaerae circulis, et eorum officiis dicendum. Ut autem in diffinitionibus praeambulis dictum est, circulis in sphaera maior est, qui commune cum sphaera centrum habens ipsam per aequalia partitur. Minor vero, qui extra centrum sphaerae sortitur centrum, et Sphaeram dividit in portiones inaequales.
Aequator igitur est circulus maior in sphaera communes cum mundo polos, et communem axem habens: nunquam situm mutans secundum planam superficiem. Dicitur et aequinoctialis, quoniam diei noctem adaequat: et cingulum primi mobilis, quoniam medius inter polos coelum cingit.
De Zodiaco.
Zodiacus sive signifer est circulus maior in sphaera oblique secans aequinoctialem, ad angulum, qui quartam partem habet recti et quasi nonagesimam. Et ideo dicitur circulus obliquus, in cuius superficie Sol contra motum primum ab occasu ad ortum defertur. Item et Luna et caeteri planetae: quanquam utrinque aliquantum exorbitantes: mediam enim semitam tenet Sol, quae ecliptica dicitur. Huius [S:10] autem declinatio ab aequatore, secundum diversas observationes, varia inventa est. Ptolemaeus hanc fecit graduum 23 minutias 511/3. Albategnius autem graduum 23 minutias 35. Alcmaeon graduum 23 minutias 331/2. Georgius Peurbachius graduum 23 minutias 28. Et Ioannes eius discipulus eam posuit graduum 23 et dimidii. Quae varietas ex motu octavae sphaerae, quem trepidatioris vocant, provenire putatur.Porro longitudines et latitudines planetarum et astrorum in hoc circulo computantur. Sicut et eorum motus cum solari motu colligantiam quandam et regulam (de qua postea dicendum est) servant. Sicut autem aequator ad primum motum, ita Zodiacus ad secundarios pertinet.
Scholium
Dividitur autem Zodiacus, in 12 arcus aequales, quae signa dicuntur, sex quidem ab aequatore borealia, et totidem australia, quorum nomina sunt Aries, Taurus, Gemini, Cancer, Leo, Virgo, Libra, Scorpius, Sagittarius, Capricornus, Aquarius, Pisces: sub quibus computatur motus luminarium, et planetarum. Quorum nomina sumuntur a constellationibus octavae: quae a priscis astronomis putabatur primum mobile. Postea vero quam a Ptolemaeo deprehensus est motus eius tardus ab occasu in ortum contrarius primo motui, opus fuit computare hunc motum tardum in superiori coelo, et in eo intelligi Zodiacum, sitque tale coelum, primum mobile. Idem sequitur propter motum trepidationis, quem commentus est Tebitius. Quoniam vero Alphonsus ipsi octavo coelo adscripsit utrunque motum, scilicet longitudinis, ac trepidationis; oportuit adiungere sphaeram decimam cum tertio Zodiaco, in quo computarentur omnes motus secundarii, hoc est, nonae in longitudine, octavae secundum trepidationem, et septem successive planetarum, ut ipsum decimum sit. Primum mobile, quod oportet unico motu ferri, contranitentibus inferioribus.
De duobus tropicis.
Tropici sunt duo circuli in Sphaera aequatoris paralleli, et Zodiacum in duobus punctis tangentes: et perinde inter se aequales: determinantes maximum Solis ab aequatore secessum, in dictis punctis, a quibus Sol convertitur ad Aequatorem. Et ideo Tropici dicuntur. Hic per Cancri, ille per Capricorni principium. Hic nobis hyematis, ille aestivus.
De punctis aequinoctiorum, et solstitiorum.
Aequinoctialis autem et Zodiacus se vicissim per aequalia, hoc est in semicirculos dispescunt. Et puncta sectionum dicuntur Aequinoctia, eo quid in illis Sol Aequinoctium. Semicirculi [S:11] vero Zodiaci utrinque in punctis tropicorum tactuum in quadrantes distinguuntur, quae puncta Solstitia dicuntur: quoniam (ut dictum est) maximum ab aequatore secessum determinant. Quatuor vero quadrantes singuli continent tria signa, quae Sol perambulat per singulos menses, faciens quatuor anni tempora, scilicet Ver, Aestatem, Autumnum, et Hyemem.
De arctico, et antarctico parallelis.
Utque ratio postulat, quantum Zodiacus declinat ab aequinoctiali; tantum et illius poli ab huius polis secedunt. Itaque duo circuli minores per Zodiaci polos descripti, et aequatori aequidistantes, iamque inter se aequales, dicuntur Arcticus et Antarcticus. Ille quidem ab ursa septentrionali, hic a contraria positione denominatus.
De quinque Zonis.
Per dictos quinque parallelos, tam in coelo, quam in terra distinguuntur zonae totidem, ut scilicet illa, quae tropicis interiacet, dicatur torrida, propter Solis continue praesentis aestum. Duae autem extremae ab arctico et antarctico circulis, circum polos inclusae, quae potius sphaericae portiones dicendae sunt, quam zonae, dicantur frigidae, propter Solis maximam distantiam, glacie perpetua horrescentes. Duae demum inter has et torridam relictae, quoniam hinc algorem, illinc calorem participant, temperatae vocitentur. Sed nonnulli, sicut Polybio placuit, torridam in duas per aequatorem partiuntur: ut sic fiat senarius zonarum numerus, ut sicut binae sunt frigidae, binae temperatae, ita et totidem ponantur torridae.
De coluris duobus.
Duos quoque circulos maiores in superficie sphaerae intelligimus, per utrunque mundi polum ductos. Quorum alter per puncta solstitiorum, reliquus per puncta aequinoctiorum incedit. Inde nomina sortitos, ut ille solstitialis, hic aequinoctialis colurus dicatur. Ille et per zodiaci polos transit: quandoquidem et per puncta contactuum tropicorum. Unde tam aequatoris, quam zodiaci semicirculos singulos per aequalia dispescit, ut in praeambulis patuit. Qui, quoniam sunt circuli declinationum, idcirco non solum praedicta quatuor cardinalia puncta indicant, sed maximas etiam Solis declinationes, polorum distantias, ac zonarum latitudines metiuntur. Videntur autem hi duo circuli totam sphaerae machinam, ac circulorum contextum sustinere. Cumque incedant per polos aequinoctialis, et ille vicissim per horum polos deducitur. A quibus tota sphaerica superficies in octona sphae[S:12]ralia triangula, ex tribus singula quadrantibus constituta distinguitur. Dicuntur vero coluri quoniam nobis imperfecti et mutili apparent. Sunt enim ex eis portiones quaedam circa polum occultum, quae nunquam exoriuntur, tanto quidem maiores, quanto est obliquior horizon.
De motu primo.
Cum autem tota coeli machina virtute primi motus, continue volvatur ab ortu in occasum, regulariter: sequitur ut ex tali motu astra omnia, et singula caeli puncta describant in uno ambitu, singulos parallelos circulos. Quorum ille sit maior, qui a polo remotior. Unde et inter eos aequinoctialis erit maximus: horum periferiae in eodem tempore, sive per aequa temporum intervalla descriptae sunt similes, in circulis autem aequis aequales. Si autem per inaequalia temporum intervalla describantur, erunt temporibus proportionales.
De divisione circuli.
Omnis autem in sphaera circulus tam maior, quam minor secatur primum in sex portiones, quoniam semidiameter sexies repetitus chordas facit talium portionum, hoc est, sena hexagoni latera. Quae portiones appellantur physica signa. Et rursus haec singula secantur in sexagenos gradus. Gradus autem singuli in totidem minutias. Et minutiae deinceps in eiusdem numeri partes. Signum autem commune est dimidium signi physici. Unde cum circulus contineat signa communia duodecim, congrue annus in totidem menses dividitur. Ut sicut de motu Solis circulus integer debetur anno; ita signum respondeat mensi, et gradus diei. Quamvis non ad amussim motum tempori (ut verba nostra sonant) ille mundi opifex accomodaverit, neque lunatio praecise mensem metiatur commendatur hic Alphonsus qui diem, aut colligendo multiplicans, aut diminuendo dividens processit, sicut in divisione circuli per sexagenarium numerum, scilicet ut tempus motui in proportione respondens faciliorem redderet calculum. Sed de motu diurno, sicut integer circulus perficitur in die, ita quindeni gradus in horis singulis. Et arcus reliqui proportionaliter. Horae autem datum est signi dimidium, ut tam diei, quam nocti duodenarius horarum numerus adscriberetur: quot videlicet sunt zodiaci signa, vel anni menses. Hora autem temporalis est duodecima pars diei, vel noctis.
De Horizonte.
Horizon est circulus maior, qui manifestum hemisphaerium ab occulta disterminat. Cuius polus est vertex loci, vel zenit oculi inspectoris. Unde antipodes habent eundem horizontem: sed sub op[S:13]positis verticibus diversa spactant hemisphaeria. Rectus horizon est, qui per Mundi polos transit, et ideo orthogonaliter secat aequinoctialem. Obliquus autem horizon est, qui oblique secat eundem, et cui polorum unus elevatur, ac reliquus tantundem deprimitur.
De meridiano.
Meridianus est circulus maior, per loci verticem et per mundi polos incedens. Qui quoniam singulos parallelorum arcus, tam super horizontem, quam sub eo receptos per aequalia dividit, ideo tam instans meridiei, quam mediae noctis semper determinat. In hoc altitudines meridianae, et per eas altitudo aequinoctialis, declinatio astri, et latitudo regionis per quadrantem captatur. Si quidem circulus hic est et altitudinis, et declinationis circulus, cum per horizontis et per aequatoris polos incedat.
De circulis altitudinum.
Circulus altitudinis est circulus maior ductus per horizontis polos et locum astri. Altitudo astri est arcus circuli altitudinis inter locum stellae et horizontem.
De Umbris.
Umbra recta est, quam stylus ad horizontem perpendicularis proiicit in ipsum horizontis planum. Quae nulla est, dum Sol verticem loci possidet: infinita vero, dum horizontem. Umbra versa est, quam stylus ad planum circuli verticalis perpendicularis in ipsum planum, Sole meridianum possidente, proiicit. Quae nulla est, dum Sol infimus: infinita, dum altissimus. Unde, cum Solis altitudo habet dimidiam recti anguli; utraque umbrarum aequiperat stylum suum. Item notandum, quod circulus verticalis est, qui per zenit regionis, perque sectiones horizontis et aequatoris ducitur. Et umbra versa est, quam stylus cylindri pendentis ad Solem vergens in ipsa cylindrica superficie deorsum proiicit. Sol igitur elevatior umbram rectam minorem, versam vero longiorem facit.
De loco astri, longitudine, latitudine, ascensione, ac declinatione.
Linea veri loci stellae vel astri est, quae a centro terrae per centrum astri usque ad concavam primi mobilis superficiem producitur. Locus astri est punctum, quod dicta linea in dicta superficie indicat. Circulus latitudinis astri est, qui per zodiaci polos et astri locum incedit. Longitudo astri, seu verus motus est arcus zodiaci a sectione verna, hoc est ab Arietis initio, secundum signorum successionem, usque ad circulum [S:14] latitudinis receptus. Latitudo astri est arcus circuli latitudinis inter astri locum et zodiacum sumptus, septentrionalis vel meridionalis a polo denominatus, ad quem vergit. Haec enim pertinent ad zodiacum, in quo et cuius respectu longitudines et latitudines secundum motus secundarios computantur. Circulus autem declinationis est, qui per mundi polos et astri locum describitur. Recta stellae vel astri ascensio est arcus aequinoctialis a sectione verna, secundum successionem usque ad circulum declinationis receptus. Declinatio stellae est arcus circuli declinationis inter locum stellae et aequinoctialem clausus septentrionem vel austrum versus mensuratus. Unde patet quod colurus solstitialis (quoniam per polos mundi et zodiaci transit) est tam latitudinis, quam declinationis circulus. Et quoniam omnis declinationis circulus est horizon rectus, idcirco talis circulus determinat rectam stellae ascensionem, quae et ipsa recta descensio est. Similiter et obliquus horizon determinabit in stella obliquam ascensionem, ac descensionem. Differentia vero, sive excessus rectae et obliquae ascensionum, dicitur differentia ascensionalis: et est arcus, sive periferia, in qua semidiurnus arcus stellae excedit quadrantem, vel exceditur a quadrante circuli. Qui arcus computatur in aequatore, vel in parallelo stellae. Quare, si stella existat in aequatore, nulla est praedicta ascensionum differentia. Et tunc semidiurnus arcus stellae quadrans est praecise: quoniam aequator aequat arcum nocturnum diurno. Et haec pertinent ad aequatorem: cuius respectu et in quo mensurantur ascensiones et descensiones, atque declinationes secundum motum primi mobilis. Ascensio autem vel descensio arcus zodiaci, vel signi, est arcus aequatoris ei cooriens, vel cooccidens, sive coascendens, vel condescendens.
De situ horizontis recti.
Sub Aequatore degentibus omnes arcus, diurni sunt nocturnis aequales. Omnes stellae oriuntur et occidunt. Et umbra recta versus quatuor mundi plagas proiicitur, et bis in anno nulla est, dum scilicet Sol in aequatore constitutus per eorum verticem fertur.
De situ obliqui horizontis.
Sub omni parallelo versus polum manifestum bis tantum in anno dies aequatur nocti. Et dies aestivi sunt hybernis longiores: noctes autem breviores, quanto scilicet ab aequinoctio Sol remotior. Et quaedam stellae semper apparentes, quaedam semper occultae. Et latitudo loci aequalis altitudini poli. Item sub remotiori parallelo ab aequatore fit maior dierum ac noctium inaequalitas; maiorque numerus stellarum semper apparentium, maior etiam semper delitescentium. [S:15]
De situ degentium inter aequinoctialem et tropicum.
Inter aequinoctialem, et tropicum degentibus umbra recta quadrifariam porrigitur, et bis in anno nulla est: bis enim in anno Sol per eorum verticem transit.
De situ degentium sub tropico.
Sub tropico degentibus semel in anno nulla fit umbra meridiana. Semel enim in anno, scilicet in tropico positus per eorum zenit incedit, alias semper ad partes poli extantis umbra flectitur.
De situ degentium inter tropicum et arcticum, vel antarcticum circulum.
Inter tropicum et arcticum, vel antarcticum viciniorem, scilicet habitantibus, umbra meridiana semper ad partes poli manifesti extenditur: nunquam enim Sol per eorum zenit defertur.
De situ degentium sub Arctico et Antarctico.
Sub Arctico, vel contraposito habitantibus semel in anno dies viginti quatuor horarum est, et nox unius instantis. Semel etiam nox viginti quatuor horarum, et dies unius instantis. Et umbra recta super horizontem circumquaque flectitur. Et quoniam tropici tangunt talem horizontem, ideo in tropico extante includitur quidquid non occidit, in reliquo quidquid stellarum non exoritur.
De situ sub polo mundi degentium.
Mundi polum pro vertice habentibus, dimidium sphaerae semper apparet. Et dimidium reliquum semper delitescit annique dimidium dies continua; et reliquum dimidium nox est continua. Horizon enim illorum est aequinoctialis. Et umbra circumfertur in circularem ambitum.
De ascensionibus signorum in horizonte recto.
In horizonte recto, quatuor signa punctis aequinoctialibus contigua sortiuntur aequas inter se, et minimas ascensiones. Quatuor autem sequentia aequales et mediocres. Quatuor reliqua utrinque ad solstitialem punctum desinentia aequales, et maximas. Ita enim poscit ratio triangulorum sphaeralium.
De ascensionibus signorum in horizonte obliquo.
At in horizonte obliquo, duo signa uni puncto aequinoctii conti[S:16]gua habent invicem aequales et minimas ascensiones. Duo autem sequentia invicem aequales et mediocres. Duo demum ad terminos solstitiorum desinentia invicem aequas et maximas. Verum, si conferantur signa opposita, illud quod in semicirculo zodiaci ascendente, maiorem habet ascensionem. Intellige autem semicirculum ascendentem eum qui rectius ascendit.
Corollaria
Duo signa opposita in quolibet horizonte, habent ascensiones simul iunctas aequales aggregato ascensionum rectarum suarum.
Arcus coalterni dierum, ac noctium in quolibet horizonte sunt invicem aequales.
De die ac nocte maxima zenit habentium inter arcticum circulum, mundique polum.
Zenit habentibus inter arcticum circulum mundique polum, dies maximus continuatur per totum illud tempus, in quo Sol moratur in illo arcu zodiaci, qui nunquam occidit. Contra, nox maxima continuabitur per tantum tempus, quantum Sol moram trahet in opposito et aequali arcu zodiaci, qui semper delitescit. Punctum autem solstitii mediat talem arcum. Unde dies illis vel nox maxima continebit tot dies, quot gradus habebit talis arcus.
De ascensionum, vel descensionum mora.
Signa igitur, seu arcus zodiaci aequas invicem ascensiones sortiti, peroriuntur in temporibus aequis. Arcus vero maiorem sortitus ascensionem, in maiori tempore oritur. Idemque de descensionibus dicendum. Unde, quoniam in qualibet die vel nocte (quantumcunque sit) oriuntur sex signa, et totidem occidunt: idcirco in longissima die vel nocte oriuntur sex signa tardissimae ascensionis, et occidunt sex signa reliqua tardissimae descensiones. Contrarium vero fit in die, vel nocte brevissima. Unde sequitur, ut habentibus zenit sub arctico vel antarctico circulo, sub ipsum solstitium, in die longissima (quae viginti quatuor horarum est) sive in nocte alterius solstitii totidem horas habente, oriantur sex signa et totidem occidant. In nocte autem illius solstitii, aut in die huius (quae instans temporis est) in instanti oriantur sex signa, et totidem occidant. Et id, quoniam quotidie zodiacus counitur horizonti, et in instanti secatur ab eo. [S:17]
De perioecis.
Perioeci, hoc est, sub eodem parallelo circumhabitantes habent eandem et eiusdem poli altitudinem, aequales et eorundem signorum ascensiones, sive descensiones, aequos arcus eiusdem loci diurnos, sive nocturnos, aequales simul umbras: eandem simul aeris temperiem, item ortuum et occasuum anticipationem, secundum intervallum longitudinum. Nam in caeteris, sivet in his fit anticipatio meridiei, secundum idem intervallum.
De antoecis.
Antoeci autem, hoc est, in contrapositis et aequalibus parallelis habitantes, habent aequales, sed diversorum polorum altitudines: aequales in oppositis signis ascensiones et descensiones: aequales arcus, sive diurnos, sive nocturnos, sed in oppositis locis: aequales temporum dispositiones, sed in oppositis signis. Unde quando hi vernum, illi autunnale tempus: quando aestivum hi, brumale tempus illi sortiuntur.
De antipodibus.
Antipodes, sive antichthones, sunt non solum Antoeci, sed etiam per diametrum oppositi. Quare conferuntur in omnibus, sicut antoeci. Verum habent etiam eundem horizontem, sed diversa hemisphaeria, et contra positos in axe horizontis vertices. Unde quidquid oritur his, occidit illis: et econtrario. Item quidquid stellarum semper apparet nobis; apud nostros antoecos, et antipodes semper delitescit, et econtrario.
De amphisciis, perisciis et antisciis.
Amphiscii sunt, quibus meridianae umbrae utroque proiiciuntur, ut intra tropicos positis. Periscii autem, quibus umbrae in circulum flectuntur: velut intra circulum articum, vel sub polo constituti. Antiscii vero, quibus umbrae meridianae in contrarias partes distenduntur, sicut antoecis contingit. Et notandum, quod situs praedicti comprehenduntur per longitudines et latitudines locorum: de quibus dicendum.
De longitudinibus, et latitudinibus locorum.
Exordium longitudinum in sua Geographia sumpsit Ptolemaeus a meridiano insularum fortunatarum, utpote Occidentis habitati extremo termino. Itaque longitudo loci, est arcus Aequatoris, aut eius paralleli a praedicto meridiano versus ortum, usque ad talis loci meridianum computatus. Nam Mundum describentes septentrionalia superne locamus; et a sinistris dextrorsum, hoc est, ab Occidente in Orien[S:18]tem procedimus. Latitudo autem loci est arcus meridiani inter Aequatorem, et locum ipsum comprehensus, habens nomen a Septentrione, vel ab Austro, quorsum scilicet locus ab Aequatore secedit. Unde loci aequalium et eiusdem nominis latitudinum sunt periaecorum. Loci autem aequalium et diversi nominis latitudinum sunt antoecorum: et tunc si eorum longitudines differant per semicirculum, sunt antipodum. Latitudo autem semper poli celsitudinem aequiperat.
De ortu et occasu astrorum.
Stellae ortus matutinus est, qui fit oriente Sole. Vespertinus vero, fit dum Sol occidit. Item occasus stellae matutinus ad ortum Solis: vespertinus ad occasum fit. Similiter coeli mediatio per eundem respectum ad Solem nomina sortietur. Hos ortus, aut occasus quidam cosmicum, et chronicum vocant. Sed diffinitio rem indicat, non vocabulum.
De climatibus.
Climata sunt paralleli praecipui habitationum, qui dinstinguuntur a Ptolemaeo secundum crementa diei maximi. Ponitur autem medium primi climatis in parallelo: ubi maximus dies habet horas 13 qui per Meroen insulam transit. Secundi climatis medium in parallelo habente maximum diem horarum 131/2 qui per Syenem urbem transit. Tertii climatis medium in parallelo diei maximi horarum 14 qui per Alexandriam. Quarti climatis medium in parallelo horarum 141/2 qui per Rodum. Quinti climatis medium in parallelo diei maximi horarum 15 qui per Romam. Sexti climatis medium in parallelo diei maximi horarum 151/2 qui per Borysthonem. Septimi climatis medium in parallelo diei maximi horarum 16 qui transit per Rhipheos montes. Horum principia et fines distinguuntur per crementa quadrantum horae in maximis diebus. Vide Geographiam Ptolemaei, et Pappi mundum. Nunc de apparitionibus et occultationibus astrorum paucis dicendum est.
De apparitionibus, et occultationibus stellarum.
Apparent primum stellae propter secessionem earum a Sole. Occultantur autem propter accessum. Apparitio dici potest ortus heliacus, vel prima fulsio. Sed occultatio, dicetur occasus heliacus, vel postrema fulsio. Stellae quidem fixae ac tardiores Planetae, propter Solis, qui velocior est, ad eas accessum, occultantur occasu heliaco vespertino, quae postrema fulsio vespertina dicitur. Deinde propter Solis ab eis recessu *** apparent ortu heliaco matutino: quae prima fulsio matutina dicetur. Luna vero ad Solem, qui tardior est, acce[S:19]dens, occultatur occasu heliaco matutino: quae postrema fulsio matutina vocatur. Deinde, propter eius a Sole secessum, apparet ortu heliaco vespertino: quae prima fulsio vespertina vocabitur. At Venus, et Mercurius, quando sunt directi (quoniam velociores Sole) occidunt, et occultantur occasu heliaco matutino, propter eorum accessum ad Solem, facientes postremam fulsionem matutinam. Et deinde recedentes a Sole, apparent ortu heliaco vespertino, facientes primam fulsionem vespertinam: sicut Luna faciebat, quae Sole velocior. Quando autem Venus, et Mercurius sunt tardiores Sole, et retrogradi: tunc, propter Solis ad eos, et eorum ad Solem accessum, occultantur occasu heliaco vespertino, facientes postremam fulsionem vespertinam. Deinde, propter Solis ab eis, et eorum a Sole discessum, apparent ortu heliaco matutino, facientes primam fulsionem matutinam: sicut stellae fixae et planetae superiores, Sole tardiores faciebant. Et est notandum, quod astrum minoris luminis postulat maius a Sole intervallum, ut appareat. Et Luna potest occultari mane vetus, et deinde apparere vesperi nova eodem die (quod innuit author Theoricarum) ac ratione et experimento comprobatum est. Fallitur ergo Plinius et quicunque aliter sentiunt.
De motu Solis.
Hactenus de his, quae pertinent ad motum primum. Nunc de secundariis motibus principia quaedam libanda sunt. Et primum de Sole. Sol defertur ab eccentrico deferente, super centro proprio regulariter: et ideo super quocunque alio puncto, et super centro Mundi inaequaliter. Linea recta per haec duo centra incedens, dicetur augis linea: it enim per punctum deferentis a centro Mundi remotissimum, quod dicitur aux: et per vicinissimum, quod dicitur oppositum augis. Linea medii motus Solis, est, quae a centro mundi ad zodiacum ducta aequidistat lineae a centro deferentis ad centrum Solis ductae. Aequatio Solis, est arcus zodiaci inter lineas veri et medii motuum: quae nulla est, dum Sol in auge, vel in eius oppositio sistitur: maxima vero in longitudinibus mediis. Aux Solis, sicut et reliquorum planetarum movetur ad motum octavae sphaerae.
De motu Lunae.
Luna defertur ab epicyclo, superne contra successionem signorum. Epicyclus vectatur a deferente eccentrico super centro mundi regulariter. In coniunctionibus luminarium, secundum medios motus, centrum epicycli sistitur in auge deferentis. Inde centrum epicycli versus ortum, et aux eccentrici versus occasum sic moventur, ut linea medii motus Solis semper media sit. Unde in quadraturis, centrum [S:20] epicycli sistetur in opposito augis eccentrici: et in oppositione rursus in auge. Propter talem augis motum, centrum deferentis describit periferiam circuli parui circa centrum Mundi. Illud autem punctum, in quo talis periferia secat lineam augis, est centrum aequantis motum Lunae in epicyclo. Nam linea, quae ab istoc puncto per centrum epicycli ducitur, indicat augem mediam epicycli, a qua Luna in epicyclo semper regulariter elongatur. Aux autem vera epicycli per lineam a centro Mundi per centrum epicycli ductam terminatur. Et arcus epicycli inter duas auges dicitur aequatio centri: quae nulla est, dum centrum epicycli, in auge deferentis, aut in eius opposito fuerit: maxima vero in longitudinibus mediis. Centrum Lunae est elongatio centri epicycli ab auge eccentrici. Argumentum medium, elongatio Lunae ab auge epicycli media. Verum autem a vera. Aequatio argumenti est arcus zodiaci inter lineas medii et veri motuum. Linea medii motus a centro mundi per centrum epicycli ducitur. Et aequationes argumenti scriptae in tabulis supponunt epicyclum in auge deferentis. Quas pro aliis sitibus opus est adaugere secundum proportionem minutorum proportionalium ad 60 parte sumpta de diversitate diametri, quae maximus excessus est.
De motu trium superiorum et Veneris.
Quilibet trium superiorum et Venus defertur in epicyclo superne secundum successionem signorum. Epicyclus autem defertur a deferente eccentrico. Centrum deferentis, est in loco medio inter centrum mundi et centrum aequantis. Linea a centro aequantis per centrum epicycli, determinat augem mediam epicycli. Quae autem a centro mundi per centrum epicycli, monstrat locum epicycli verum. Quae autem a centro mundi educta aequidistat ductae a centro aequantis per centrum epicycli, est linea medii motus planetae, vel epicycli. Arcus zodiaci inter lineas medii et veri motus epicycli, dicitur aequatio centri in zodiaco: cui semper similis est arcus epicycli inter duas auges: qui dicitur aequatio centri in epicyclo. Per has aequationes ex centro et argumento mediis eliciuntur vera. Deinde per aequationem argumenti, quae est arcus zodiaci inter verum locum epicycli et verum locum planetae adaequatur verus locus planetae. Et in trium superiorum quolibet tantum elongatur planeta ab auge epicycli media, quantum Sol a loco planetae medio. Aequationes autem argumentorum scriptae in tabulis supponunt epicyclum in media longitudine eccentrici. Pro caeteris autem sitibus versus augem oportet subtrahi, et versus oppositum superaddi portiones quasdam de diversitatibus diametri, secundum proportionem minutorum proportionalium ad 60 sumptas. Venus [S:21] autem et Mercurius sic colligantur cum Sole, ut ipsorum trium idem semper sit medius motus. Et eorum media coniunctio perpetua. Auges autem feruntur secundum motum stellarum fixarum.
De Mercurio.
Notandum, quod in Mercurio centrum aequantis est medium inter centrum Mundi, centrumque parvi circuli. In cuius periferia defertur centrum deferentis contra successionem signorum cum tenore motus planetae medii. Et quoniam dicta periferia it per centrum aequantis, idcirco centrum, deferentis semel in anno counitur centro aequantis. Caetera per Mercurio definiuntur et supputantur sicut in aliis planetis.
De directionibus regressionibus et stationibus.
Quilibet autem quinque errantium in superiori parte epicycli fertur secundum successionem signorum. In interiore contra. In Luna fit contrarium. Duae autem lineae a centro Mundi eductae secantes epicyclum utrinque a linea per centrum, in duobus inferiorum, sectionum punctis determinant stationes.
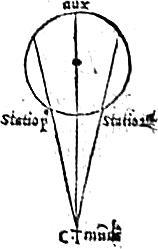
In puncto orientali planeta de directo fit retrogradus. In occidentali de retrogrado fit directus. Illud punctum statio prima: hoc autem statio secunda nuncupatur. In illo motus planetae in epicyclo incipit vincere motum deferentis epicyclum. In hoc autem vinci ab eo unde in toto arcu epicycli superiore planeta est directus. In interiore autem retrogradus est. Luna vero non patitur regressionem, sed motus tantum intensionem, aut remissionem. Quia motus deferentis non vincitur a motu Lunae in epicyclo, sed tantum intenditur, aut retardatur.
De latitudine Lunae et Planetarum.
Notandum quod deferens Lunae secat viam Solis, hoc est ecly[S:22]pticam. Et puncta sectionum dicuntur caput et cauda Draconis, sive Anabibazon et Catabibazon, hoc est ascensus et descensus. Quae puncta moventur contra successionem signorum quotidie per tres minutias gradus fere. Epicyclus autem Lunae iacet in plano deferentis. Et maxima latitudo deferentis, est graduum quinque invariabilis semper. Deferentes quoque singuli trium superiorum planetarum declinant ab eclyptica. Et punctum maximae declinationis in Marte est in auge deferentis. In Saturno ante augem per gradus 50. In Iove post augem per gradus 20. Et epicyclus inclinatur magis et minus ad deferentem. Sed dum centrum epicycli est in nodis; epicyclus iacet in plano eclipticae. Alibi diameter, super quam fit inclinatio epicycli, aequidistat ut eclipticae. Et maxima inclinatio fit in punctis maximarum declinationum. Aux autem epicycli semper interiacet superficiebus eclypticae ac deferentis. At deferentes duorum inferiorum deviant mobiliter ab eclyptica, hinc et inde super diametro longitudinum mediarum. Epicycli autem inclinantur et reflectuntur ad deferentes, super diametros erectas et transversas, cum hac regula. Centro epicycli in nodis constituto, eccentricus unitus iacet eclypticae, qui a nulla est deviatio deferentis. Et tunc in epicyclo reflexio nulla est: inclinatio autem maxima. Sed centro epicycli punctum deferentis maxime devians, tenente, tam deferentis deviatio, quam epicycli reflexio est maxima: inclinatio vero nulla. In locis autem mediis crescunt et decrescunt pro cremento latitudinum. Motus autem in Venere septentrionem et ortum: in Mercurio austrum et occasum poscit in primis semicirculis: in secundis contrarium. Sicut Georgius in Theoricis latius explicat. Ex his colligitur, latitudo singulorum planetarum ab eclyptica secundum situm epicycli in deferente, et planetae in epicyclo. In Luna vero latitudo supputatur per solam deferentis declinationem, quandoquidem epicyclus nihil ab eius planitie flectitur.
De loco viso astri, et diversitate aspectus.
Motus visus astri consideratur secundum visum nostrum in terrae superficie positum. Linea loci visi est, quae ab oculo nostro per centrum astri usque ad concavam primi mobilis superficiem extenditur. Visus astri locus est punctum, quod indicat dicta linea in dicta superficie. Diversitas aspectus astris est arcus circuli altitudinis inter verum et visum locum. Unde si astrum sit in vertice horizontis; talis diversitas nulla est. Ibi enim eadem est linea veri et visi loci. In horizonte autem si ponatur astrum, diversitas est maxima: quae consideratur inde secundum longitudinem et latitudinem zodiaci. Visibilis coniunctio astrorum dicitur, secundum locos visos. [S:23]
De eclipsibus.
Eclipsis Solis nihil aliud est, quam visibilis eius cum Luna coniunctio. Hoc est Lunae inter visum nostrum et Solem interpositio. Sicut cum Luna videtur obiectu suo aliquem nobis ex planetis, vel aliquam ex stellis intercipere, quod saepe contingit. Unde, propter diversitatem aspectus, in diversis terrae locis diversam, accidit, ut si Luna totum nobis Solem obtegat, tunc in locis magis septentrionalibus, aut australibus, partem illius coelet, aut ex eo nihil abscondat. Atque ita Solis eclipsis nobis fiat universalis; alicubi partialis, et alibi nulla, non secus ac si nubes Solem velaret. Sed Lunae eclipsis est verus luminis defectus. Fit enim, cum Luna in plenilunio ingreditur aut tota, aut partim in umbram terrae. Et sic tota vel partim privatur lumine Solis et tantundem deficit vere, ac deficere videtur omnibus in locis, in quibus apparet. Eclypsis igitur Solis sit in coniunctione, eclypsis Lunae, et in oppositione luminarium, tunc scilicet, cum coniunctio, vel oppositio contingit iuxta eclypticam, hoc est iuxta nodos seu puncta sectionum: in quibus lunaris deferens secat eclypticam, sicut theoricarum authores et tabularum canones docent. Ubi termini eclypsium diffiniuntur ut puta digiti, minuta casus, minuta morae, et tempora durationum. Assignantur autem limites, hoc est distantiae a nodis, intra quos possibile est eclypsim fieri aut Solis, aut Lunae. Et arctiores adhuc termini, qui necessitatem induceret, quamvis neglecti ab authoribus. Et notandum, quod Sol aut Luna in sex mensibus: item Luna in quinque mensibus. Et tunc Sol in diversi locis. Item Sol in semptem mensibus. Et in uno mense in contrapositis locis, potest bis eclypsim pati. Potest et intra quindecim dies utrunque luminarium deficere. Sol, scilicet in coniunctione, et Luna in oppositione.
De motu octavae spherae.
Ex numero autem motuum arguitur numerus caelorum, sive orbium caelestium. Unde certum est, luminaria et erraticos quinque singulis motibus delatos sortiri caelos singulos. Ut sic octavum caelum (si motum secundarium non habeat, ut vetustissimi astronomorum putabant) ponatur primum mobile. Sed, qui a Ptolemaeo suas cum anteriorum observationibus conferente, deprehensum est stellas fixas moveri versus Orientem singulis gradibus per annos centenos; et inde a Tebitio, ferri per motum trepidationis: idcirco necessarium fuit primum motum adscribi non caelo. Deinde quoniam Alfonsus motui trepidationis addidit motum longitudinis; oportuit unum ex his, scilicet trepidationem proprium esse octavae: motum autem longitudinis attribui non caelo, atque ita motum primum relinqui decimo. Quando [S:24] quidem necesse est supremum coelum simplici motu ferri. Quod, si Alfonsi positio vera est, possent nonus et decimus orbis vocari, quasi deferentes et membra octavi: ut trium orbium aggregatum contineatur sub uno firmamenti vocabulo. Itaque cum vetustissimi nondum deprehendissent motum octavae: ac Ptolemaeus animadvertisset tardissimum unius gradus in annis centenis motum: deinde Albategnius in annis 66 per unum gradum ferri; Tebitius, ut salvaret hanc varietatem et maximarum Solis declinationum, primus commentus est trepidationis motum. Alfonsus vero, sive observatione, sive calculi coniectura inductus adierit trepidationi longitudinem. Tebitius dixit capita Arietis et Librae octavi caeli circumferri in periferiis parvorum circulorum: quorum poli sint principia Arietis et Librae noni caeli. Quo motu fit, ut eclyptica mobilis octavi caeli super aliis atque aliis punctis secans aequinoctialem, ob respectum talis sectionis (quae periodus est motuum) et ob ipsum circularem ambitum, fecerit apparere motus diversitatem in stellis fixis. Aequatio octavae sphaerae secundum Tebitium, est arcus Zodiaci mobilis inter principium Arietis, et punctum sectionis Zodiaci cum aequatore. Argumentum autem motus trepidationis est, arcus parvi circuli inter aequatorem et principium Arietis mobilis. Ponit autem Tebitium. Capita Cancri et Capricorni octavae inseparabilia ab eclyptica nonae. Alfonsus autem dixit capita Arietis et Librae octavi coeli ferri in periferiis parvorum circulorum, quorum poli sunt capita Arietis et Librae noni coeli, in spatio 7 millium annorum per integrum ambitum. Dictos autem polos cum circulis, hoc est, totum nonum moveri per totum ambitum Zodiaci primi mobilis in spatio 49 millium annorum: ita ut arcus Zodiaci primi mobilis a principio Arietis primi mobilis secundum successionem computatus usque ad caput Arietis nonae, sive polum parvi circuli, dicatur motus longitudinis nonae. Arcus autem parvi circuli a supremo puncto versus Septentrionem usque ad caput Arietis octavae, dicatur argumentum motus accessus, et recessus, sive trepidationis octavae. Arcus demum eclypticae noni inter polum parvi circuli et circulum per polos eclypticae nonae et caput Arieti octavae interceptus, dicatur aequatio octavae spherae. De quo latius in Theoricis. Vide Peurbastrium quo ad speculationem: quo vero ad calculum consule Alfonsum et Blanstrinum.
De numero, et ordine spherarum.
Necesse est igitur coelos non pauciores esse, quam novem, ut scilicet supremus sortiatur motum primum, ab oriente in occidentem. Octo autem reliqui totidem singuli motus secundarios. Primum stellarum fixarum, quae unico motu ad orientem feruntur. Et semptem reliquos [S:25] planetarum: quorum ordinem vetustissimi philosophi ita posuerunt, ut nunc tenemus: ut scilicet sphaera fixarum suprema sit: proxima Saturni: quem sequitur Iuppiter, Iovem Mars, hunc sequitur Sol superior Venere, et post Mercurium Luna infima. Posteri vero, sicut Plato, quia nec Veneris, nec Mercurii interiectu Solis eclypsim fieri videbant; eos supra Solem locandos esse censuerunt. Alpetragnius autem, qui motuum diversitates per incurtationem quandam primi motus fieri putabat, sub Marte Venerem, sub qua Solem et inde Mercurium statuebat. Minus enim incurtat Venus a motu primo, quam Sol ex parte quidem epicycli. Mercurius autem plusquam Sol. Harum opinionum antiquissimam recentiores, ut verissimam susceperunt: quandoquidem nec Venus (cuius superficies subcentupla Soli ponitur ab Albategnio) Solem, et minus Mercurius obtenebrare sensibiliter potest. Amplius maxima lunae a centro Mundi distantia semidiametrum Terrae 64 vicibus: minima vero Solis indidem remotio eandem diametrum 1070 vicibus continet. Unde sequitur, ut interstitium orbium luminarium semidiametrum Terrae 1006 vicibus contineat. Quod cum natura non sinat vacuum, iure Veneris ac Mercurii orbibus adscribetur: ne tanta moles vacua sinatur. Venerem autem Mercurio superiorem esse, nos in Cosmographiae nostrae dialogis pulcherrimis coniecturis, et argumentis demonstravimus. [S:26]
Ad Lectorem.
Non tamen haec scripsimus, candide Lector, ut, contemptis caeteris, nostra tantum legeres: sed quo per nostram traditionem melius caetera intelligeres, et ab aliis omissa perdisceres. Nec dubito, quin ex nostris elementis, cautius sis lecturus, et acutius iudicaturus quidquid apud Sacroboscum, Robertum, aut Campanum videris. Sed nec Robertus, Sacrobosci, nec Campanus Roberti lectionem exclusit, uti fortasse credidit. Sicut nec Theoricae Peurbachii, quamvis exactissimae, et secundum Ptolemaicam doctrinam traditae efficere potuerunt, ut Alpetragrii dogmata, et Cremonensia delyramenta penitus excluderentur. Satisque, fuit Georgio et Regimundo admonuisse lectores, ut quid cavendum, quidve approbandum esset, optime cognoscerent. Sed omnia perperam tradita emendare omnium animos ad rectitudinem convertere nequidem Atlas, qui coelum sustinet, totis viribus valeret. Toleratur et Nicolaus Copernicus, qui Solem fixum ac Terram in girum circunverti posuit: et scutica potius, aut flagello, quam reprehensione dignus est. Transeamus igitur ad reliqua, ne tempus frustra teramus.