Programma e materiale relativo al corso essere reperito in rete selezionando nella Pagina del Dipartimento la voce Materiale Didattico (http://WWW.dm.unipi.it/didactics/home.html) e quindi selezionando ALTRI CORSI DI LAUREA e Corso di laurea *****
------------------------------------------------------------- ESERCIZIO n. 1 Un punto si muove su una retta in modo che la distanza dal punto iniziale è proporzionale al quadrato del tempo percorso. In due minuti percorre dodici metri. Si trovi la velocità media: a- nei primi cinque minuti, b- tra il quarto minuto e il settimo.
------------------------------------------------------------- ESERCIZIO n. 2 a- Calcolare le derivate delle seguenti funzioni
![]()
![]()
b- Calcolare
![]() se
se ![]() ,
e se
,
e se ![]() calcolare
calcolare ![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 3 a- Si trovi la tangente nel punto ![]() dell'insieme
di punti del piano definito da
dell'insieme
di punti del piano definito da ![]()
b- Si trovino le tangenti nel punto ![]() dell'insieme del piano
definito da
dell'insieme del piano
definito da
![]() .
.
c- Si trovi l'angolo di incidenza in ![]() tra le due curve
tra le due curve ![]() ,
,
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 4 a- Si provino le relazioni
![]() ,
,
![]() .
.
b- Si provi che per ![]() si ha
si ha
![]() ,
,
![]() .
.
------------------------------------------------------------- ESERCIZIO n. 5 Si studino i grafici delle seguenti funzioni
![]() .
-------------------------------------------------------------
ESERCIZIO n. 6 a- Si studi la derivabilità della funzione
definita da
.
-------------------------------------------------------------
ESERCIZIO n. 6 a- Si studi la derivabilità della funzione
definita da
![]() se
se ![]() , e nulla per
, e nulla per ![]() .
.
b- Si studi la derivabilità della funzione
definita da
![]() se
se ![]() , e nulla per
, e nulla per ![]() .
.
* c- Sia
![]() se
se ![]() ,
, ![]() .
Si provi che esiste
.
Si provi che esiste ![]() ed è
strettamente positiva, ma la funzione non è crescente
in nessun intervallo contenente
ed è
strettamente positiva, ma la funzione non è crescente
in nessun intervallo contenente ![]() .
.
------------------------------------------------------------- ESERCIZIO n. 7 a- Tra i triangoli rettangoli di ipotenusa di lunghezza assegnata quali hanno area massima?
b- Si trovi il rettangolo con lati paralleli agli assi cartesiani, interamente contenuto in
![]() di area massima.
di area massima.
c- Tra i prismi regolari a base triangolare di volume assegnato
![]() quali rendono minima l'area superficiale?
quali rendono minima l'area superficiale?
------------------------------------------------------------- ESERCIZIO n. 8 Si calcolino se esistono i seguenti limiti:
![]()
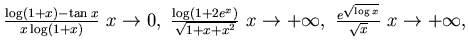
![]()
-------------------------------------------------------------
ESERCIZIO n. 9 Sia
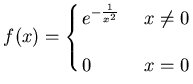 . a - Si provi che
. a - Si provi che ![]() è continua su
è continua su ![]() .
.
b - Si provi che le derivate di ![]() in
in
![]() sono del
tipo funzione razionale moltiplicato
sono del
tipo funzione razionale moltiplicato ![]() .
.
c - Si provi che ![]() è derivabile infinite volte in
è derivabile infinite volte in ![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 10 a- Si provi che la derivata del prodotto di ![]() funzioni è la somma dei prodotti delle derivate di ognuna delle funzioni
per le rimanenti funzioni:
funzioni è la somma dei prodotti delle derivate di ognuna delle funzioni
per le rimanenti funzioni:
![]()
a - Si provi
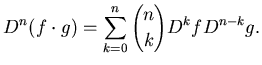
b- Si supponga che la funzione ![]() abbia
abbia ![]() derivate nel punto
derivate nel punto ![]() e che la funzione
e che la funzione ![]() abbia
abbia ![]() derivate in
derivate in ![]() . Si provi che la funzione
composta
. Si provi che la funzione
composta
![]() ha
ha ![]() derivate nel punto
derivate nel punto ![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 11 a- Sapendo che ![]() è una funzione con la derivata prima e seconda
continue e sapendo che
è una funzione con la derivata prima e seconda
continue e sapendo che
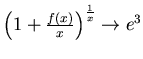 quando
quando ![]() si
calcolino
si
calcolino ![]() ,
, ![]() ,
,
![]() .
.
* b- Si provi che se ![]() su un intervallo
su un intervallo ![]() allora
allora
![]() assume tutti valori compresi tra il suo estremo superiore e il suo estremo inferiore
sull'intervallo
assume tutti valori compresi tra il suo estremo superiore e il suo estremo inferiore
sull'intervallo ![]() . In particolare la funzione
. In particolare la funzione ![]() non potrà avere discontinuità
di tipo ``salto''.
(Si consideri un'opportuna funzione che abbia come valori i coefficienti angolari
delle corde sul grafico di
non potrà avere discontinuità
di tipo ``salto''.
(Si consideri un'opportuna funzione che abbia come valori i coefficienti angolari
delle corde sul grafico di ![]() ed un estremo nei punti
ed un estremo nei punti ![]() nella prima metà
dell'intervallo
nella prima metà
dell'intervallo ![]() , ed un estremo in
, ed un estremo in ![]() nella seconda parte).
nella seconda parte).
-------------------------------------------------------------
ESERCIZIO n. 12 a- Si disegni la curva
![]() .
.
b- Si disegni a curva
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 13 Sia
![]() . Soprovi che la funzione è bigettiva da
. Soprovi che la funzione è bigettiva da
![]() in se. Detta
in se. Detta ![]() la sua inversa si calcoli
la sua inversa si calcoli
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 14 a-
Sia
![]() . Si provi che è bigettiva da
. Si provi che è bigettiva da ![]() in se.
in se.
b- Detta ![]() l'inversa di
l'inversa di ![]() si provi che
si provi che
![]() quando
quando ![]() .
.
* c- si determini esplicitamente una funzione ![]() per cui
per cui
![]() quando
quando ![]() . (Si provi
. (Si provi
![]() ).
).
-------------------------------------------------------------
ESERCIZIO n. 15 Si scriva ![]() come differenza di due funzioni convesse.
come differenza di due funzioni convesse.
-------------------------------------------------------------
ESERCIZIO n. 16 Si consideri l'equazione
![]() .
Si provi che ha una sola soluzione positiva
.
Si provi che ha una sola soluzione positiva ![]() . Si provi che
. Si provi che ![]() .
Si provi che
.
Si provi che
![]() . Usando la convessità di
. Usando la convessità di ![]() si provi inoltre
che
si provi inoltre
che
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 17 Si mostri che le uniche funzioni ![]() per cui
per cui
![]() sono le funzioni
sono le funzioni
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 18
-------------------------------------------------------------
ESERCIZIO n. 19
-------------------------------------------------------------
-------------------------------------------------------------
ESERCIZIO n. 21
-------------------------------------------------------------
ESERCIZIO n. 22
-------------------------------------------------------------
ESERCIZIO n. 23