Programma e materiale relativo al corso essere reperito in rete selezionando nella Pagina del Dipartimento la voce Materiale Didattico (http://WWW.dm.unipi.it/didactics/home.html) e quindi selezionando ALTRI CORSI DI LAUREA e Corso di laurea *****
-------------------------------------------------------------
ESERCIZIO n. 1 Usando la definizione di limite si mostri che quando
![]() si ha
si ha
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 2 Si calcolino per ![]() i limiti delle seguenti successioni al variare dei parametri
i limiti delle seguenti successioni al variare dei parametri ![]() :
:
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 3 ![]() a-
Si provi che
a-
Si provi che
![]() (diseguaglianza
tra media aritmetica e media geometrica).
(diseguaglianza
tra media aritmetica e media geometrica).
b- Si provi che per ![]() si ha
si ha
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 4 a- ![]() Si provi che se
Si provi che se ![]() allora la
media geometrica e la media aritmetica dei primi
allora la
media geometrica e la media aritmetica dei primi ![]() termini tendono ad
termini tendono ad ![]() per
per ![]() .
.
b- Si provi che se
![]() allora
allora
![]() tende a
tende a ![]() se
se ![]() a
a ![]() se
se ![]() .
.
c- Si mostri con diversi esempi che se ![]() la successione
la successione
![]() può: convergere a
può: convergere a ![]() , a
, a ![]() , ad un numero
diverso da
, ad un numero
diverso da ![]() , o non convergere affatto.
, o non convergere affatto.
d- Si provi che se
![]() allora
allora
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 5 Calcolare
per ![]() i limiti di:
i limiti di:
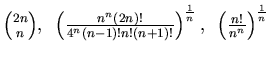 .
.
-------------------------------------------------------------
ESERCIZIO n. 6 Calcolare
per ![]() i limiti di:
i limiti di:
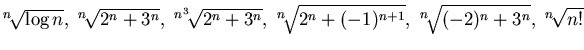 .
.
------------------------------------------------------------- ESERCIZIO n. 7 Calcolare
per ![]() i limiti di:
i limiti di:
![]() .
.
------------------------------------------------------------- ESERCIZIO n. 8 Calcolare
per ![]() i limiti di:
i limiti di:
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 9 Calcolare
per ![]() i limiti di:
i limiti di:
![]()
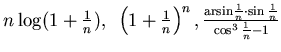 .
.
-------------------------------------------------------------
ESERCIZIO n. 10 Studiare la convergenza delle serie:
![]()
------------------------------------------------------------- ESERCIZIO n. 11 Studiare la convergenza delle serie:
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 12 Studiare la convergenza delle serie:
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 13 ![]() Si provi che
Si provi che ![]() non converge.
non converge.
-------------------------------------------------------------
ESERCIZIO n. 14 a- Si provi
![]() per
per
![]() .
.
b- Si provi che
![]() ,
per
,
per ![]() .
.
c-
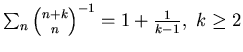 .
.
-------------------------------------------------------------
ESERCIZIO n. 15 Per quali ![]() convergono rispettivamente le serie:
convergono rispettivamente le serie:
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 16 Si considerino le successioni
![]() , e
, e
![]() .
Si provi che sono monotone, se ne calcolino
i limiti
.
Si provi che sono monotone, se ne calcolino
i limiti ![]() e
e ![]() e si studino le serie
e si studino le serie
![]() ,
, ![]() .
.
------------------------------------------------------------- ESERCIZIO n. 17 Si calcolino i seguenti limiti di funzione:
![]()
![]()
![]() .
.
------------------------------------------------------------- ESERCIZIO n. 18 Si calcolino i limiti delle seguenti funzioni:
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 19 ![]() Si calcoli usando la definizione
Si calcoli usando la definizione
![]() .
.
-------------------------------------------------------------
Definizione - Una funzione ![]() si dice Lipschitziana se esiste
una costante
si dice Lipschitziana se esiste
una costante ![]() per cui
per cui
![]() . Ovvero i rapporti incrementali sono limitati.
. Ovvero i rapporti incrementali sono limitati.
- Dato ![]() , una funzione
, una funzione ![]() si dice
si dice ![]() -Hölderiana
se esiste una costante
-Hölderiana
se esiste una costante ![]() per cui
per cui
![]() .
.
- Una funzione si dice uniformemente continua se
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 21 ![]() a- Una funzione è uniformemente continua se e solo se
per ogni coppia di successioni
a- Una funzione è uniformemente continua se e solo se
per ogni coppia di successioni ![]() ,
, ![]() se
se ![]() allora anche
allora anche
![]() .
(Si noti che non si richiede che le successioni convergano)
.
(Si noti che non si richiede che le successioni convergano)
b- Teorema Una funzione continua su un intervallo chiuso e limitato è uniformemente cont.
c- Una funzione continua che ha limite all'infinito è uniformemente continua.
------------------------------------------------------------- ESERCIZIO n. 22 a - Le funzioni Hölderiane e Lipschitziane sono uniformemente continue.
b- Il grafico di una funzione Lipschitziana si trova sempre
compreso tra due rette di pendenza ![]() e
e ![]() centrate in un qualsiasi
punto del grafico stesso.
centrate in un qualsiasi
punto del grafico stesso.
c- Si mostri che
![]() è
è
![]() -Hölderiana ma non Lipschitziana.
-Hölderiana ma non Lipschitziana.
d- Si mostri che
![]() è Lipschitziana, ma
è Lipschitziana, ma
![]() non lo è.
non lo è.
e- Si trovino funzioni Lipschitziane ma non Hölderiane. Su quali intervalli una funzione Lipschitziana è anche Hölderiana?
f-![]() Si trovi una funzione uniformemente continua
ma non Hölderiana.
Si trovi una funzione uniformemente continua
ma non Hölderiana.
-------------------------------------------------------------
ESERCIZIO n. 23 Si provi che la funzione
![]() ha massimo su
ha massimo su ![]() ma non ha minimo.
ma non ha minimo.